Conectividade estrutural

Baseada na análise do movimento das moléculas de água no tecido cerebral in vivo, a tractografia é uma moderna técnica de ressonância magnética que mostra a posição, a anatomia e a integridade dos tratos da substância branca no encéfalo e na medula, conforme a direção de suas fibras.

A Conectividade efetiva busca estudar as relações causais entre as atividades. Também é obtida por imagens funcionais. Utiliza-se Dynamic Causal Models (DCM), Causalidade de Granger entre outros métodos.

Conectividade funcional

Para análise de conectividade funcional, alguns métodos são aplicados para análise, conforme os objetivos do estudo:

• Seed-to-voxel (mapas de conectividade): Dada uma região de interesse (seed), obter um mapa de correlações com essa seed. O output é um mapa de correlação com esse ponto.

• ROI-to-ROI (grafos de conectoma) - ROI: Region of interest. O output é um grafo.

Uma das aplicações da matriz de correlação é através de grafos, com os ROIs constituindo os nós e as conexões entre cada nós as arestas, formando uma rede de conexões.

Várias propriedades destas redes são utilizadas para análise das associações entre as ROIS, por exemplo temos o grau da rede, que corresponde ao número médio de conexões da mesma, ou medidas mais locais como os hubs que representam a ROI com maior número de conexões. Assim, a partir da construção da matriz de correlação das ROIs, podemos realizar um grande número de medidas capazes de fornecer informações as redes de conectividade do cérebro humano.

Construindo computacionalmente a análise de conectividade entre ROIs.

Para um determinado voxel escolhido de semente (seed) definiremos a região de interesse a partir dele: Escolhemos o Cingulo Posterior centralizado em x=23, y=19 ,z=27 (processamos um cubo de três voxeis centralizado neste):

#Carregar a biblioteca
require(AnalyzeFMRI)

## Carregando pacotes exigidos: AnalyzeFMRI

## Carregando pacotes exigidos: R.matlab

## R.matlab v3.6.2 (2018-09-26) successfully loaded. See ?R.matlab for help.

## 
## Attaching package: 'R.matlab'

## The following objects are masked from 'package:base':
## 
##     getOption, isOpen

## Carregando pacotes exigidos: fastICA

## Carregando pacotes exigidos: tcltk

## Warning in fun(libname, pkgname): couldn't connect to display ":0"

#Leitura do arquivo
volume = f.read.volume("./data/RESTING.img")
dim(volume)

## [1]  45  54  45 450

#Dimensoes
XMAX = dim(volume)[1]
YMAX = dim(volume)[2]
ZMAX = dim(volume)[3]
TMAX = dim(volume)[4]

#Selecionar regiao-de-interesse (ROI)
#Cingulo Posterior centralizado em x=23, y=19 ,z=27
#ROI será um cubo centralizado neste voxel
SEED = array(0, TMAX)
for(ti in 1:TMAX){
  SEED[ti] = mean(volume[22:24, 18:20, 26:28, ti])
}
ts.plot(SEED)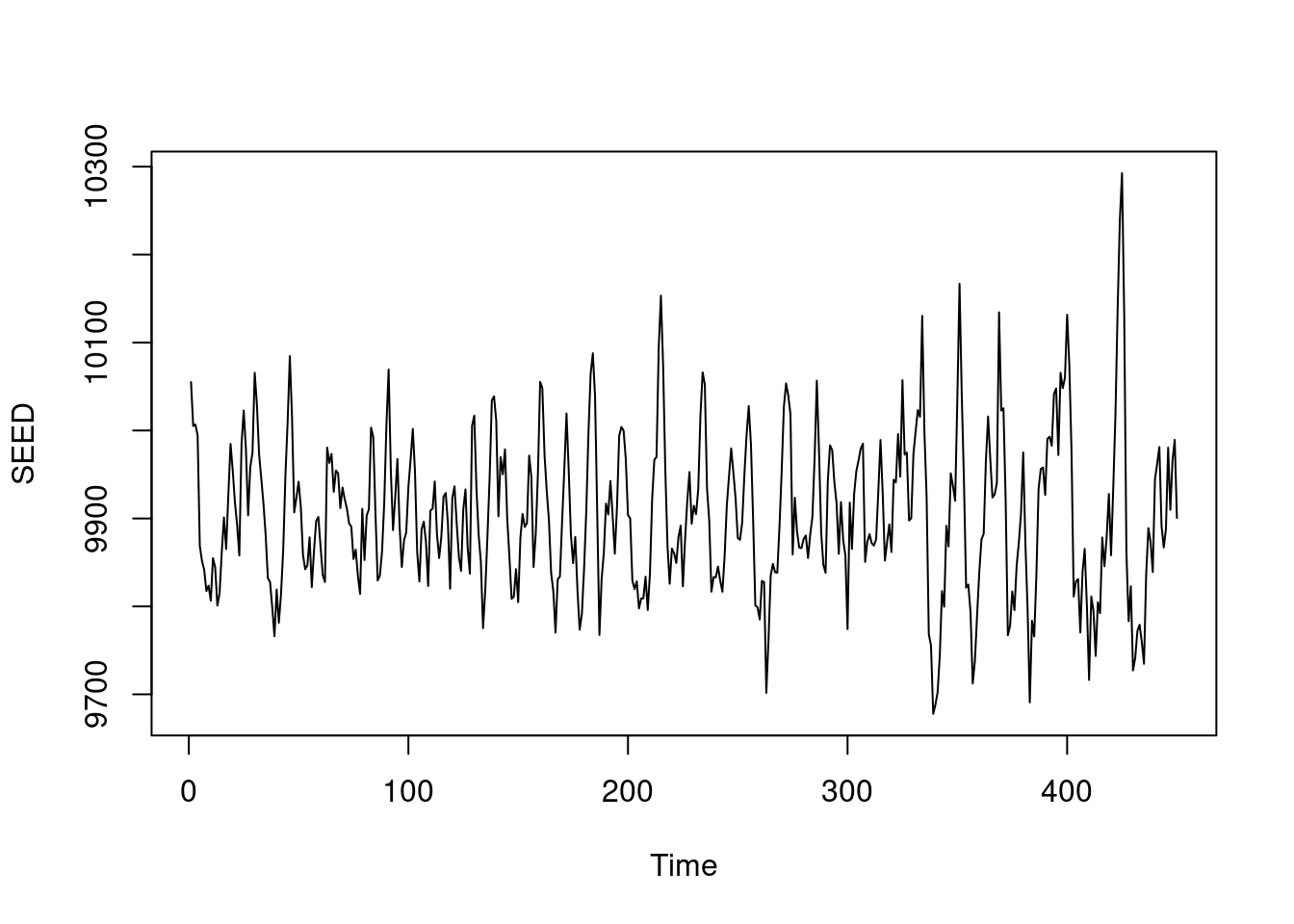

Para corrigir os artefatos sistêmicos (que podem gerar correlação espúrias), apliquemos o GSR - Global Signal Regression nos sinais BOLDs das ROIs para então recalcular a matriz de conectividade.

O Global Signal Regression é um método de correção para remoção de artefatos que consiste em ajustar um modelo de regressão linear, considerando o sinal BOLD de cada ROI como a variável resposta e o Global Signal (GS) como variável preditora: ou seja, verifica o que é comum a todos e retira o sinal global antes de calcular as correlações

É frequente realizar também (incluir como preditoras) os 6 parâmetros de movimentação da cabeça obtidos no pre-processamento. Além disso, também é comum em estudos com crianças e populações clínicas utilizar o método de scrubbing, que se baseia em descartar os scans colhidos durante grandes movimentações da cabeça.

Para calcular o GS (Global Signal), devemos normalizar o sinal BOLD das ROIS para media 0 e variância 1 (z-score), a fim de retirar a variabilidade de cada série temporal que poderia causar alguma correlação espúria.

Consideramos que essas componentes em comum estão contidas na média, por isso fazemos com que a média do sinal seja zero. Após o processo do GSR, teremos retirado, ou pelo menos minimizado, os efeitos dos artefatos sistêmicos nos sinais que poderiam causa correlações espúrias:

# Global signal - tirando a média de tudo e colocando no sinal global, deveria ser apenas nos vóxeis intracranianos

#Global signal
GSR = array(0,TMAX)
for(ti in 1:TMAX){
#na realidade deveria ser apenas dos voxels intracranianos
  GSR[ti] = mean(volume[,,,ti])
}
ts.plot(GSR)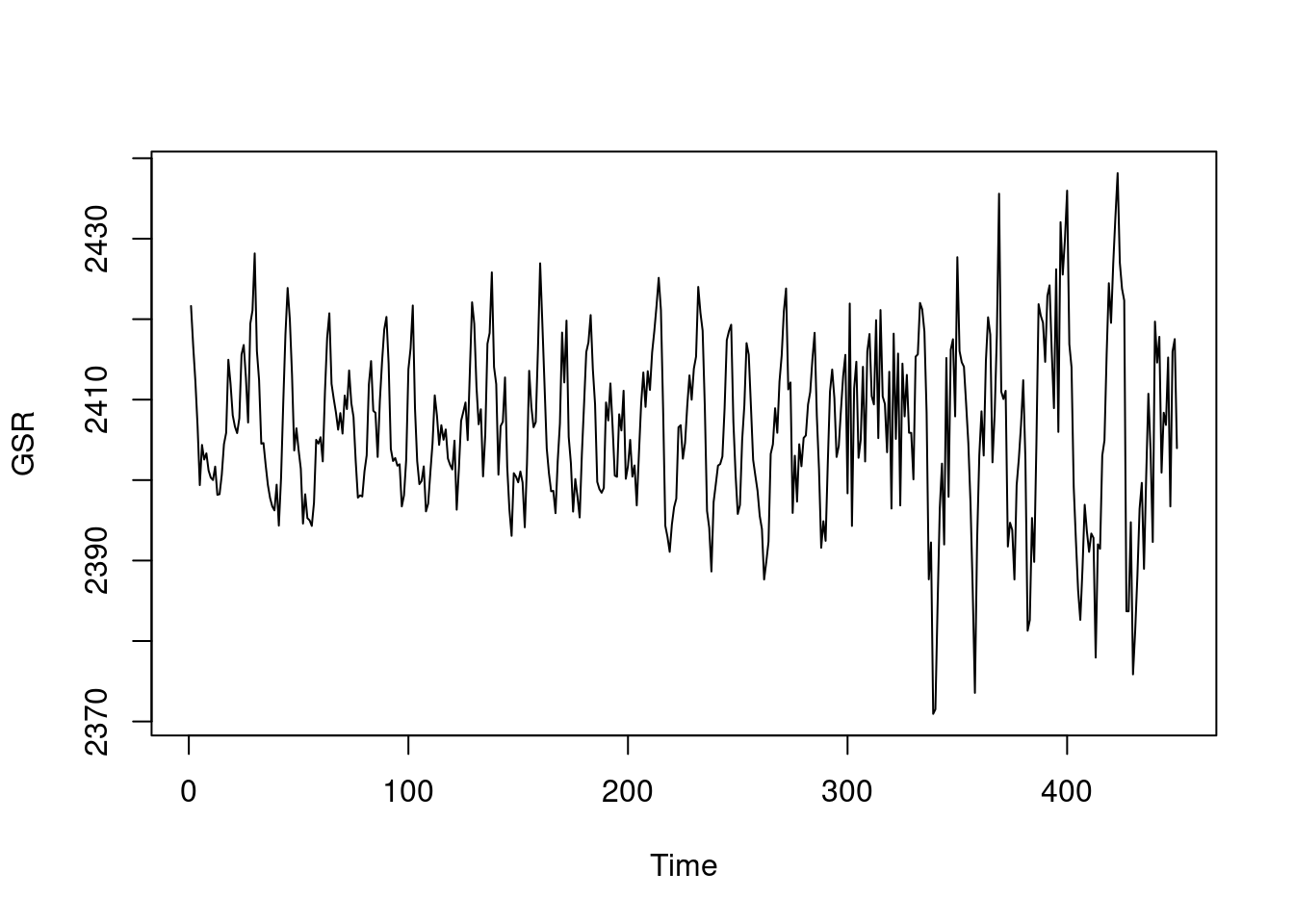

Uma vez aplicado o GSR para remoção de artefatos sistêmicos, utiliza-se o conceito de matriz de conectividade para verificar as similaridades entre as redes cerebrais de diferente indivíduos.

Podemos verificar essa semelhança entre as redes de diversas maneiras, podemos comparar as médias, máximos e/ou mínimo das correlações; ou podemos comparar as métricas de rede, como grau, coeficiente de centralidade, hubs, coeficiente de clusterização.

Para este exercício, Com 450hz numa taxa de 0.5hz, temos 900s. Armazenando o Mapa de Conectividade Funcional, com utilização do Coeficiente de correlação de Pearson:

O mapa constitui no processamento de para cada voxel a comparação com a região de interesse (SEED), armazenando os resultados de sua correlação.

MAPA = array(0, c(XMAX, YMAX, ZMAX, 1))

for(xi in 1:XMAX){
  for(yi in 1:YMAX){
    for(zi in 1:ZMAX){
       if(volume[xi, yi, zi, 1] != 0){ #mascara intracraniana
         #Coef. de Correlacao de Pearson
         MAPA[xi, yi, zi, 1] = cor(SEED, volume[xi, yi, zi,])
       }#fecha o if
}}}#fecha os for


#Salva os mapas em arquivos no formato Analyze (IMG/HDR)
f.write.analyze(MAPA,
                "MapaConectividade",
                pixdim = c(4, 4, 4),
                originator = c(23.5, 32.5, 19, 1, 1))

Olhando no MRCRO é possível ver o seed altamente ativado (porque a correlação é 1 e seu entorno possui suavização espacial, que justifica a alta ativação com a região).

#Transformacao de Fisher
z = log((1+MAPA)/(1-MAPA))
f.write.analyze(MAPA,"./data/MapaConectividadeZ",
                pixdim = c(4, 4, 4),
                originator = c(23.5, 32.5, 19, 1, 1))