Mapas de ativação e testes para fMRI

Para esse exercício, vamos utilizar dados de uma tarefa do tipo stroop. Essa tarefa consiste na medida do tempo de reação e na acurácia da leitura, em voz alta, de palavras em duas situações: 1. As palavras estão escritas na mesma cor que a cor expressa pelo significado semântico - denominamos por CONGRUENTES 2. As palavras estão numa cor que difere da cor expressa pelo significado semântico (exemplo: a palavra vermelho impressa com tinta azul) - denominamos por INCONGRUENTES

Estima-se que na segunda situação ocorre um atraso no processamento da cor da palavra, induzido pelo conflito no processamento da informação e por conseguinte, causando tempos de reação mais lentos e um aumento de erros.

Quando se trata de experimentos, o maior erro dos novatos é acreditar que com um estímulo só é possível comparar repouso com o estímulo. É necessário ter uma amostra representativa para conseguir garantir os dados para comparação.

Para análise, seguiremos os seguintes passos:

  1. Definição do block design do experimento
  2. Coleta de dados
  3. Pré-processamento do sinal: Correção do motion correction (quando a pessoa se mexe durante a aquisição de dados. Nesse caso é feito o realinhamento, com corpo rígido: 3 parâmetros rotação, 3 parâmetros de translação e/ou combinações desses movimentos).
  4. Especificar a convolução da HRF - hemodynamic response function (veremos adiante)
  5. Aplicação do GLM no sinal BOLD para cada voxel x.y.z, usando como variável preditora os dados de convoluídos
  6. Aplicação de um teste estatístico para definir quais voxels são relevantes para construção dos mapas
  7. Visualização e armazenamento dos mapas

A ideia aqui é investigar a ativação cerebral para cada uma das situações: CONGRUENTES e INCONGRUENTES. Então, primeiramente realizamos a leitura dos dados:

# Imagem esta preprocessada
# SPM (UCL) e FSL (Oxford)

require(AnalyzeFMRI)
## Carregando pacotes exigidos: AnalyzeFMRI
## Carregando pacotes exigidos: R.matlab
## R.matlab v3.6.2 (2018-09-26) successfully loaded. See ?R.matlab for help.
## 
## Attaching package: 'R.matlab'
## The following objects are masked from 'package:base':
## 
##     getOption, isOpen
## Carregando pacotes exigidos: fastICA
## Carregando pacotes exigidos: tcltk
## Warning in fun(libname, pkgname): couldn't connect to display ":0"
## 
## Attaching package: 'AnalyzeFMRI'
## The following object is masked from 'package:RNifti':
## 
##     orientation
#Leitura de dados de fMRI
volume=f.read.volume("./data/Stroop.nii")

#Leitura das condicoes (desenho experimental)
congruente=scan("./data/congruent.txt")
incongruente=scan("./data/incongruent.txt")

Obs: O comando scan é melhor (mais rápido) para ler vetor do que o read.table, mais usado para ler .txt

A função resposta ao estimulo congruente (ativação durante o estimulo, CONG = 1; e não ativação, fora do estímulo CONG = 0), como se observa em:

ts.plot(congruente)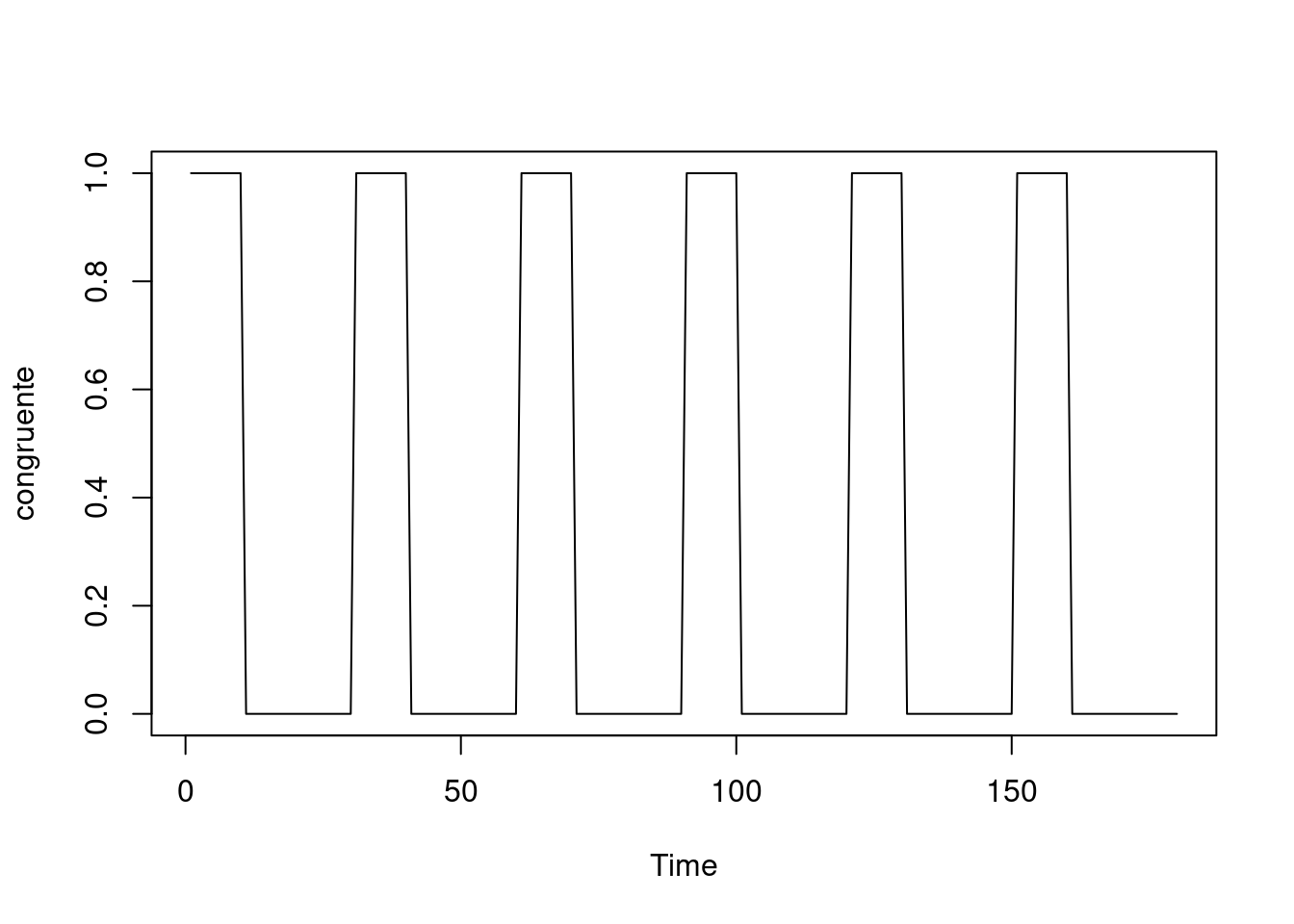

O objetivo da análise é estimar se, e em que medida, cada preditor contribui para a variabilidade observada no curso do tempo do voxel. Considere, por exemplo, uma experiência na qual a resposta BOLD, \(y\), é amostrada \(n\) vezes (ou seja, volumes). A intensidade do sinal BOLD em cada observação (\(y_i\)) pode ser modelada como a soma de um número de variáveis preditoras conhecidas (\(x_1,… x_p\)), cada uma escalonada por um parâmetro (\(\beta\)):

Realizemos agora a convolução dos estímulos sobre a resposta hemodinâmica esperada do indivíduo. Ou seja, ao ser submetido ao estimulo, espera-se que ocorra uma ativação cerebral associada a essa resposta. Essa ativação chamada de função resposta hemodinâmica (HRF – hemodinamic response functional).

A equação abaixo mostra a convolução da função resposta pela HRF pela HRF do modelo de Garry Glover:

\[ \begin{align} X[t] = \sum_{l=0}^{k} HRF[k] \hspace{1mm}* C[t-k] && \text{(sendo C a condição)} \end{align} \]

Em código, essa função dada pelo modelo de Garry Glover faz duas curvas gaussianas e a HRF é a combinação linear dessas duas gaussianas. Os parâmetros já seguem por default:

glover=function(HZ){
    a1=6
    a2=12
    b1=0.9
    b2=0.9
    d1=5.4
    d2=10.8
    c=0.35
    x=seq(0, 30, 1/HZ) # HZ is the Sampling Rate (Heartz)
    glover1=((x/d1)^a1)*exp((-x+d1)/b1)
    glover2=((x/d2)^a2)*exp((-x+d2)/b2)
    G=glover1-c*glover2
    return(G)
}

Determinando HRF: Função de resposta hemodinâmica, considerando um tempo de repetição TR de 2s, ou seja 1/2:

#HRF- Funcao de resposta hemodinamica
HRF = glover(0.5)

Exemplo de event-related (similar ao potencial evocado, vários experimentos coletados coincidindo). No caso de estímulos muito consecutivos, a curva basal nem retorna ao original, o que dificulta na visualização:

CONDICAO = array(0, 90)
CONDICAO[30] = 1
CONDICAO[60] = 1
ts.plot(CONDICAO)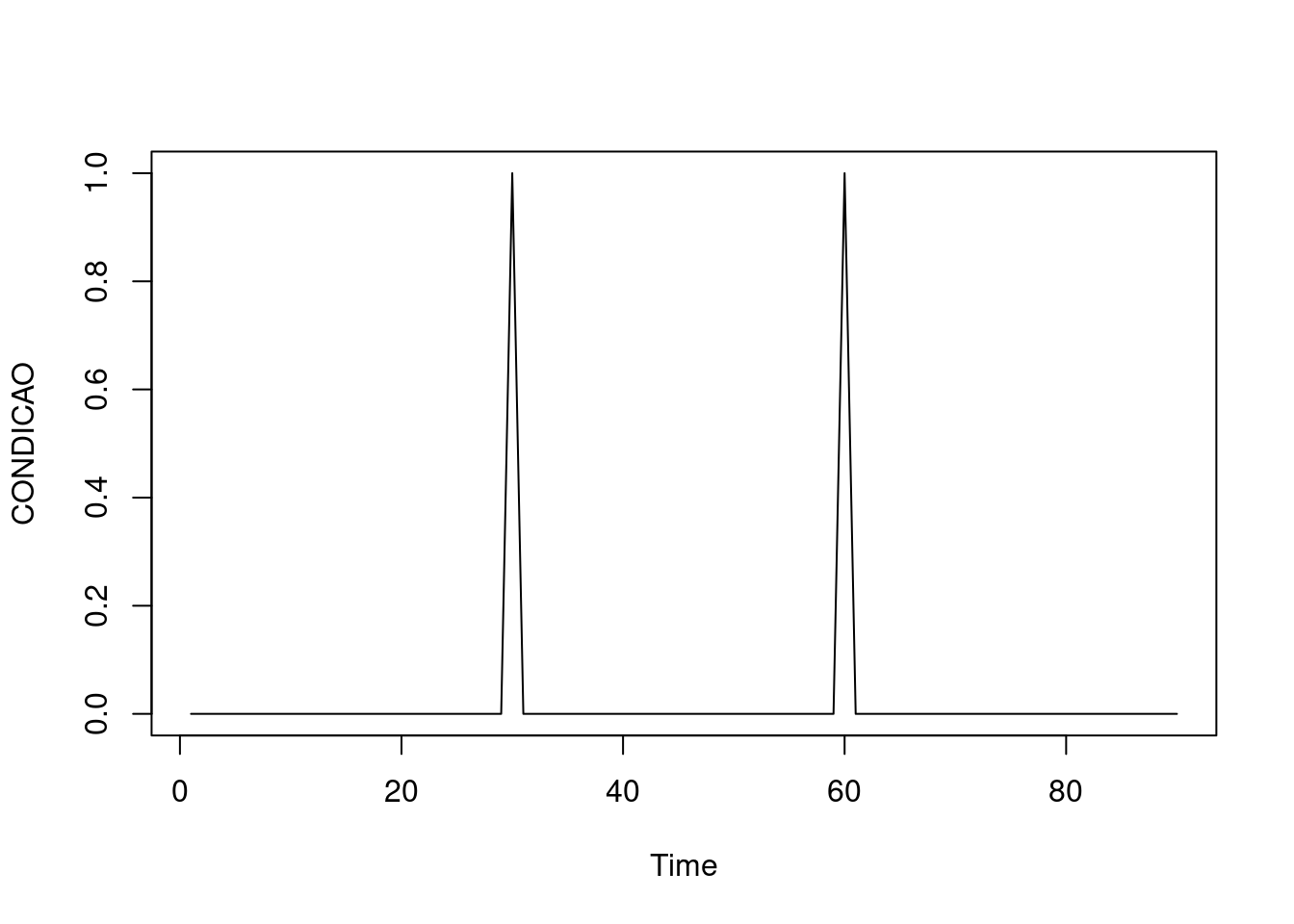

# Convolucao do vetor condicao pela HRF
# ATENCAO: NAO LER o pacote signal, pois a função
# que faz a convolução tem o mesmo nome da que faz a
# filtragem em frequência
X = filter(CONDICAO, HRF, sides=1, method="convolution")
ts.plot(cbind(CONDICAO, X), col = c(1,2))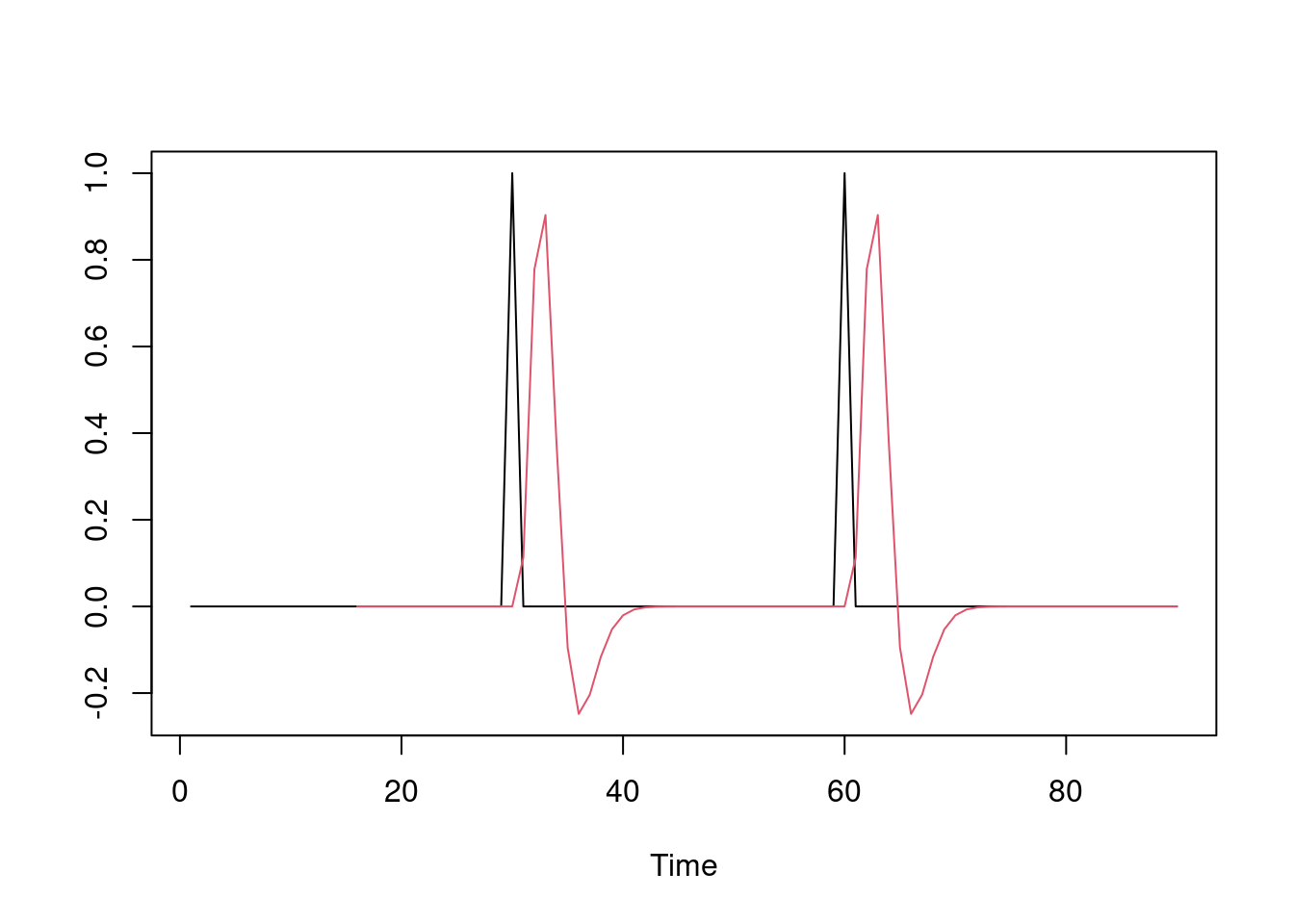

Exemplo de Desenho block-design:

CONDICAO = array(0, 90)
CONDICAO[20:40] = 1
CONDICAO[60:80] = 1
X = filter(CONDICAO, HRF, sides=1, method="convolution")
ts.plot(cbind(CONDICAO, X), col=c(1, 2))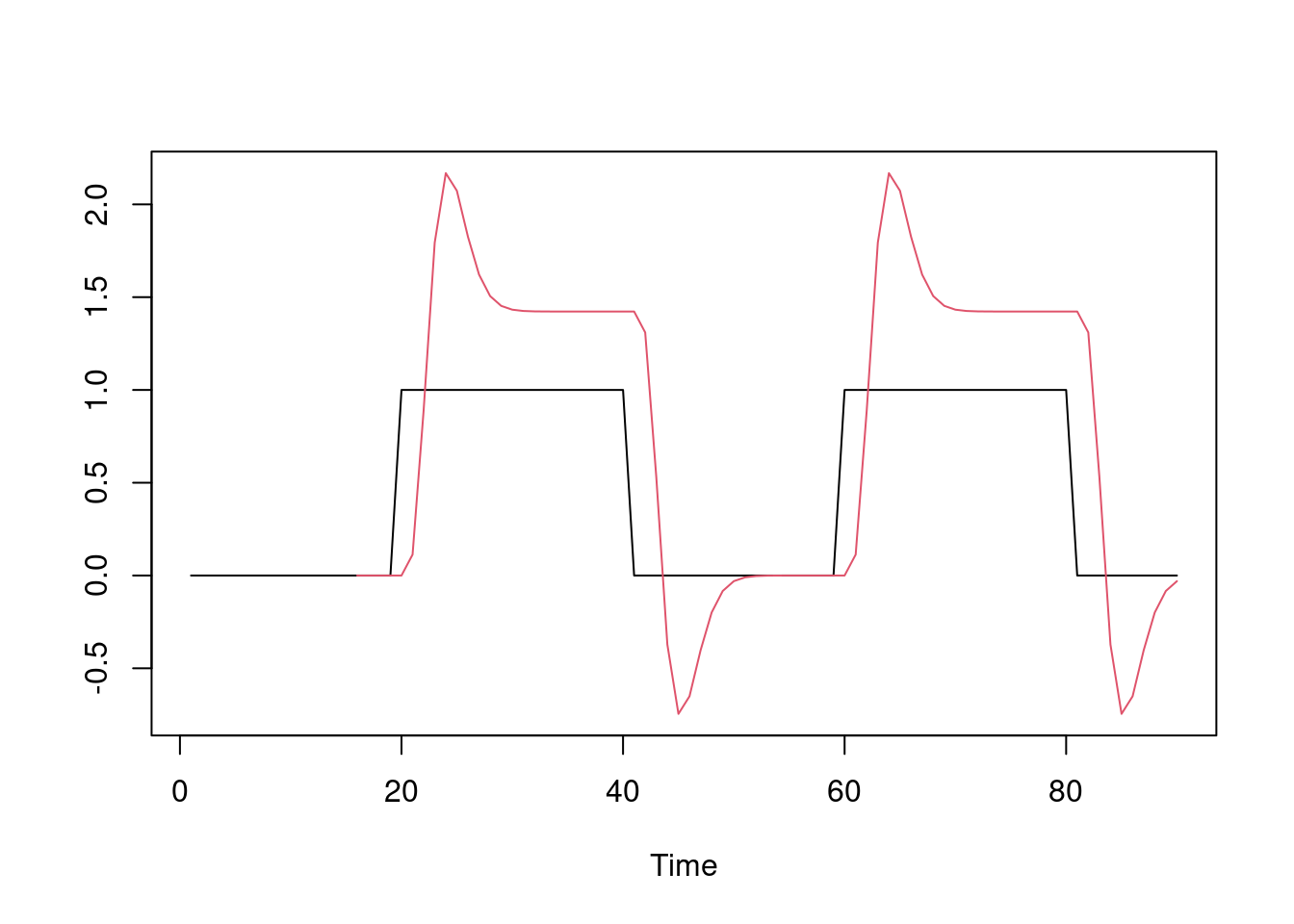

Identificando a convolução das condições pela HRF:

#Convolucao da condicao congruente pela HRF
X=filter(congruente, HRF, sides=1, method="convolution")

#Convolucao da condicao incongruente pela HRF
Z=filter(incongruente, HRF, sides=1, method="convolution")

Ao plotarmos a função que representa um modelo de ativação relacionado ao design do experimento, verificamos comportamentos semelhantes. Analisando as duas condições:

ts.plot(cbind(congruente, incongruente), col=c(1,2))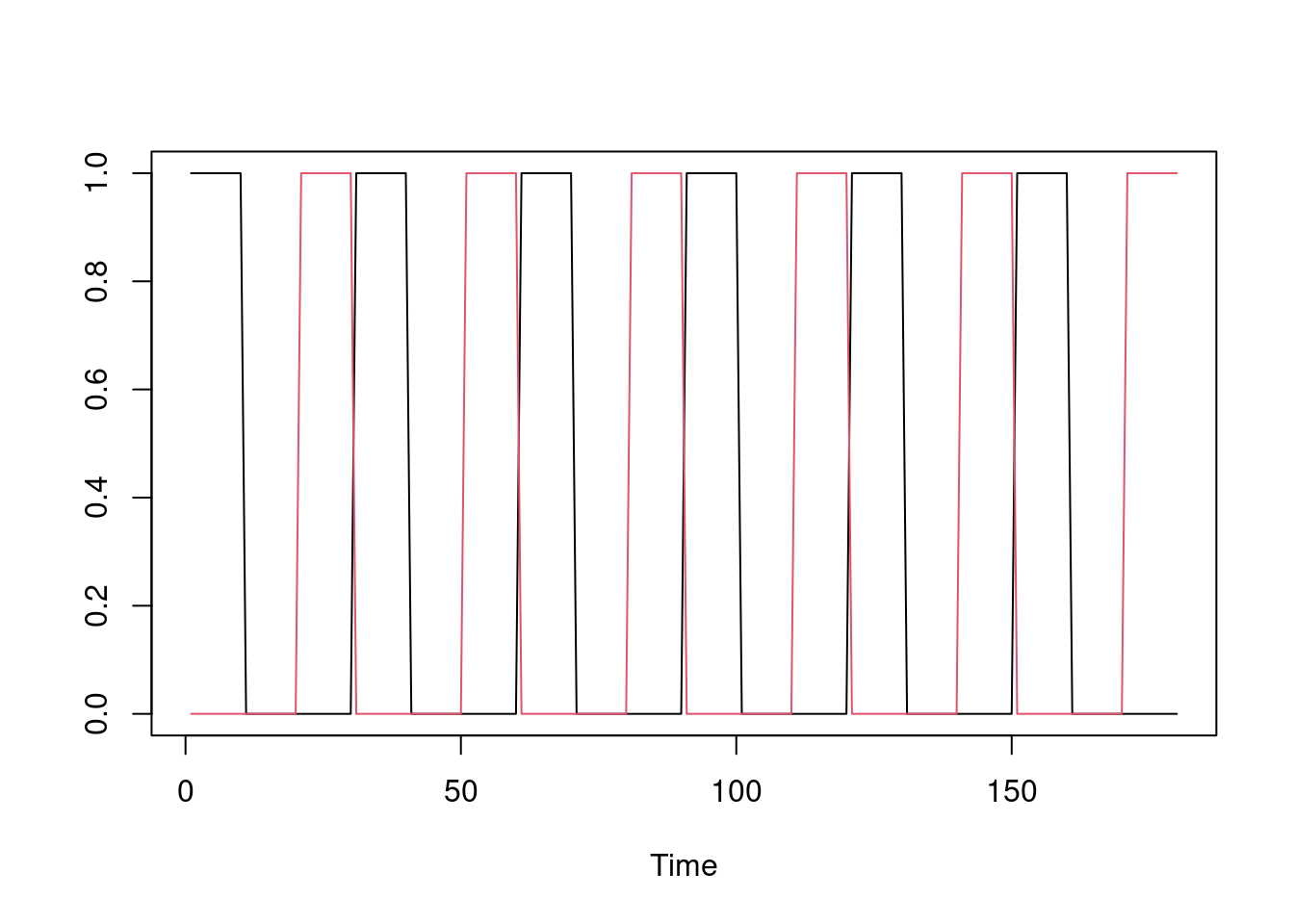

ts.plot(cbind(X, Z), col=c(1, 2))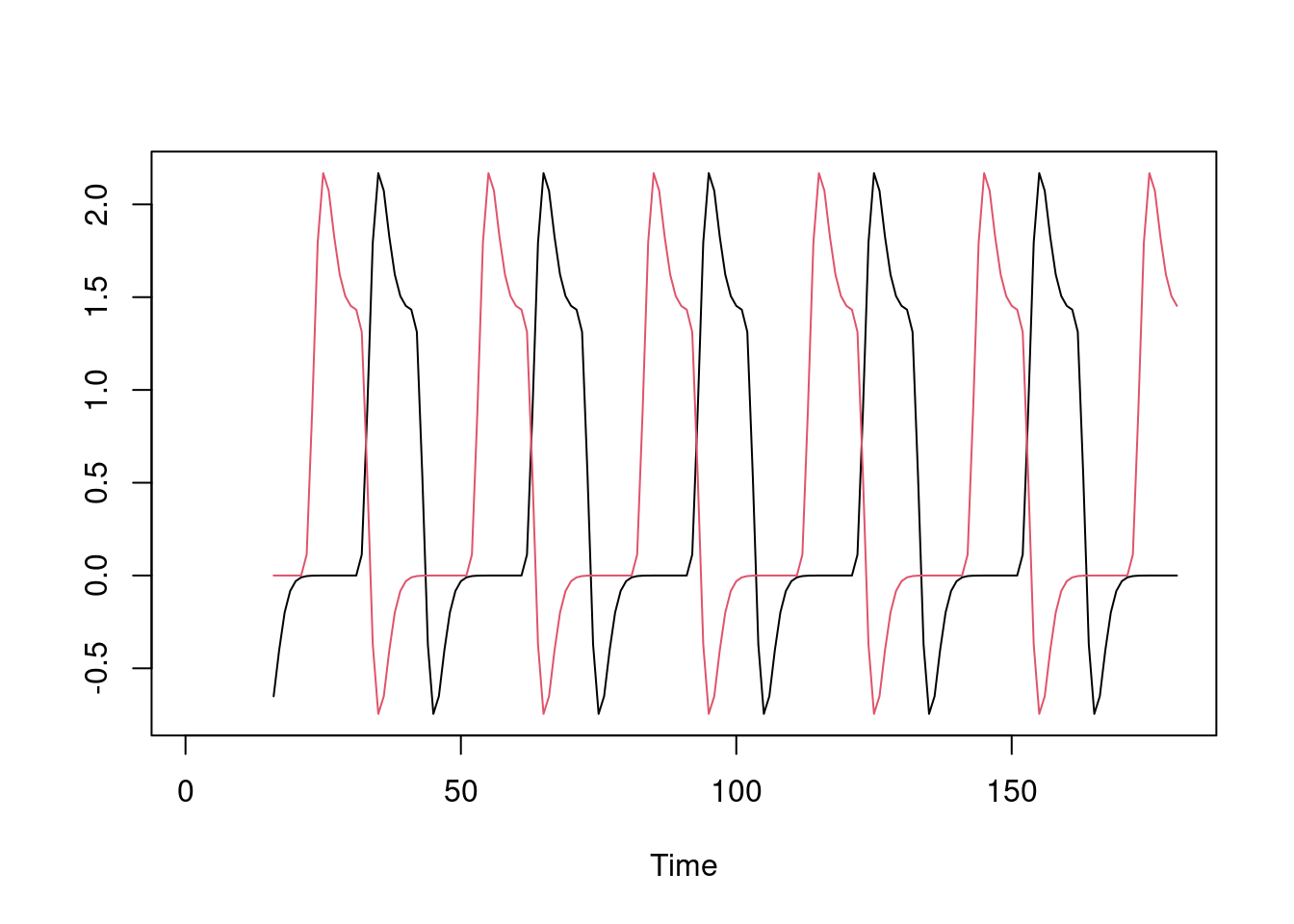

A título de curiosidade, essa convolução utilizada na função filter é equivalente ao seguinte código (as saídas são equivalentes):

#Faça a convolução do INCONG pela HRF.
Z = array(0,length(incongruente))
for(ti in (length(HRF)+1):length(incongruente)){
   for( i in 1:length(HRF)){
    Z[ti]= Z[ti]+ incongruente[ti-i]*HRF[i]
  }
}

#Convolução do CONG pela HRF
X = array(0,length(congruente))
for(ti in (length(HRF)+1):length(congruente)){
   for( i in 1:length(HRF)){
    X[ti]= X[ti]+ congruente[ti-i]*HRF[i]
  }
}

#Normalizando (colocar o máximo em 1) os dados da condição para facilitar a interpretação. 

X = X/max(X)
Z=Z/max(Z)

Para garantir uma resposta hemodinâmica mais próxima do que se espera é feita uma convolução da resposta esperada relacionada ao desenho do experimento com a função resposta hemodinâmica do modelo de Garry Glover, dando origem a um sinal convoluído que representa como seria, idealmente, o comportamento do sinal BOLD para aquele modelo de experimento.

Realizando o ajuste do modelo linear geral:

No GLM, faremos uma regressão linear múltipla onde o Y é o sinal BOLD, usando a HRF convoluída. No fundo, quero saber se o sinal se comporta conforme a ativação do voxel (se o voxel é ativado por um determinado estímulo). Para cada voxel x, y e z vamos rodar o GLM (Regressao multipla) usando como variável preditora os dados dessa convolução.

Para regressão múltipla, faremos um ajuste de nível (\(\alpha\)) e de escala (\(\beta\))

\[ \begin{align} BOLD_{x,y,z}[t] = \alpha + \beta . X_t + \epsilon_t && \text{(sendo } X_t \text{ a condição da convolução)} \end{align} \]

neste caso, supondo: \(\epsilon_t\) com média zero e variância constante (homocedasticidade) e os erros \(\epsilon_t\) são independentes

Para comparação, faremos um teste de hipóteses. Analisando pelo t-valor, estatística t (verificar ativa ou não e se é estatisticamente diferente de zero ou não): Estatística T do beta correspondente a condição congruente é igual ao do modelo.

Obs: O valor p não armazena sinal, ou seja, não conseguimos verificar existência de ativação ou de desativação.

Fazendo os Mapas de estatisticas T:

# Verificando a dimensão do volume para identificar como serão os mapas:
dim(volume)
## [1]  45  54  45 180

Considerando no caso do GLM o \(\beta_1\) o congruente e \(\beta_2\) o incongruente:

# Considera as dimensões da matriz volume e adiciona esse 1, para construção do mapa
mapaTcongruente = array(0,c(45,54,45,1))
mapaTincongruente = array(0,c(45,54,45,1))

for(xi in 1:45){
  for(yi in 1:54){
    for(zi in 1:45){
        #pega somente os voxels intracranianos, ou seja, diferentes de zero:
       if(volume[xi,yi,zi,1]!=0){
         #Ajuste do modelo linear geral - GLM:
         modelo=lm(volume[xi,yi,zi,]~X+Z)

         #Estatistica T do beta correspondente a condicao congruente
         mapaTcongruente[xi,yi,zi,1] = summary(modelo)$coef[2,3] # Beta_1

         #Estatistica T do beta correspondente a condicao incongruente
         mapaTincongruente[xi,yi,zi,1] = summary(modelo)$coef[3,3] #Beta_2
       }#fecha if
}}}#fecha for do xi,yi,zi

Se quero testar se \(beta_1\) > 0, ou seja ativação de congruente vs nêutro: \[ \begin{align} \begin{bmatrix} \\ 1 && 0 && 0 \end{bmatrix} \end{align} \]

Se quero testar se \(beta_1\) < 0, ou seja deativação de congruente vs nêutro: \[ \begin{align} \begin{bmatrix} \\ -1 && 0 && 0 \end{bmatrix} \end{align} \]

Se quero testar se \(beta_2\) < 0: \[ \begin{align} \begin{bmatrix} \\ 0 && -1 && 0 \end{bmatrix} \end{align} \]

E por fim, se quero testar a ativação Incongruente > Congruente, ou seja, \(beta_2\) > \(beta_1\), quero verificar se \(-\beta_1 + \beta_2 > 0\), logo, na condição:

\[ \begin{align} \begin{bmatrix} \\ -1 && +1 && 0 \end{bmatrix} \end{align} \]

A estatística T me diz se por exemplo os valores de \(\beta_1\) são maiores ou não que zero. Usamos um p de 0,1% para evitar os ruídos da suavização, que geram falsos positivos (t = 3.03).

Agora, armazenando os mapas em arquivos no formato Analyze (um IMG e um HDR):

f.write.analyze(mapaTcongruente, "./data/MapaCongruente", 
                pixdim = c(4, 4, 4),
                originator = c(23.5, 32.5, 19, 1, 1))
f.write.analyze(mapaTincongruente, "./data/MapaIncongruente", 
                pixdim = c(4, 4, 4),
                originator = c(23.5, 32.5, 19, 1, 1))

Um artigo muito interessante que resume o uso de GLM nas análises de fMRI: https://doi.org/10.3389/fnhum.2011.00028

Previous
Next

Last updated on Apr 18, 2022