GLM - Modelo Linear Geral
Na ressonância magnética funcional, a hemoglobina que carrega o oxigênio é chamada oxiemoglobina (oxyHb) e ao se desprender do oxigênio essa passa ser chamada desoxihemoglobina (deoxyHb). A oxyHb possui propriedade diamagnética, isto é fraca interação com outros campos magnéticos; tem momento magnético zero e nenhum elétron sem par. Já a deoxyHb é paramagnética, isto é possui maior susceptibilidade magnética, com elétrons não pareados e momento magnético significativo. Assim, na presença de um campo magnético intenso, como da ressonancia, as moleculas de deoxyHb causam uma atenuação do campo magnético e consequentemente uma alteração no contraste da imagem. Como resultado deste comportamento, tem-se o chamado sinal BOLD (Blood Oxigenated level dependent) que é medido pela ressonância magnética funcional (fMRI) - Notas de aula da Cândida.
O sinal BOLD medido na fMRI está relacionado com a variação da quantidade de deoxyHb na região de estudo. O aumento da atividade cerebral, aumenta o fluxo sanguíneo para aquela região como uma forma de suprir a demanda metabólica. As células que cuidam da estrutura cerebral são as Glias, os astrocitos (metabolismo) e os oligocitrocitos (estrutural). A presença dos oligocitrocitos causam um aumento do vasos sanguíneos, que causa o aumento do fluxo sanguíneo e consequentemente diminuição da deoxyHb e aumento da oxyHb causando um aumento no sinal BOLD, isso é chamado de acoplamento hemodinâmico. Graças ao acoplamento hemodinâmico podemos medir o sinal BOLD e associa-lo a atividade cerebral, possibilitando a realização de inferências sobre o comportamento do cérebro.
O método GLM – Modelo Linear Geral é um método estatístico utilizado para verificar como uma variável depende de outras variáveis de interesse. Neste modelo a variável dependente é escrita como uma combinação linear das variáveis independentes, onde os coeficientes dessa combinação representam. A regressão linear é utilizada em umas das análises feitas com dados de fMRI, que são os mapas de ativação. Esses mapas mostram as regiões ativadas, de indivíduos ou grupo de indivíduos, quando estão realizando alguma tarefa cognitiva.
A regressão é dada por:
e:
Para conseguir entender melhor como gerar esses mapas de ativação, abaixo segue uma melhor compreensão do modelo. Primeiro implementaremos manualmente e na sequência com o modelo já do próprio R:
Simulando um modelo linear:
# Neste caso, y não depende de x:
X = rnorm(100)
Erro = rnorm(100)
Y = 2 + 0*X + Erro
plot(X, Y)
Estimadores de MMQ para alfa e beta:
# Cria o vetor Ytil (vertical) e a matriz Xmat (design matrix)
N = 100 #arbitrario
Ytil = matrix(Y, N, 1)
# já atribuindo
Xmat = matrix(1, N, 2)
Xmat[ ,2] = X
# Faz os cálculos na multiplicação matricial
betahat = solve(t(Xmat)%*%Xmat)%*%t(Xmat)%*%Ytil
# estimador é a fórmula que traz a estimativa.
Ypredito = betahat[1]+ betahat[2]*X
plot(X, Y)
lines(X, Ypredito, col=2)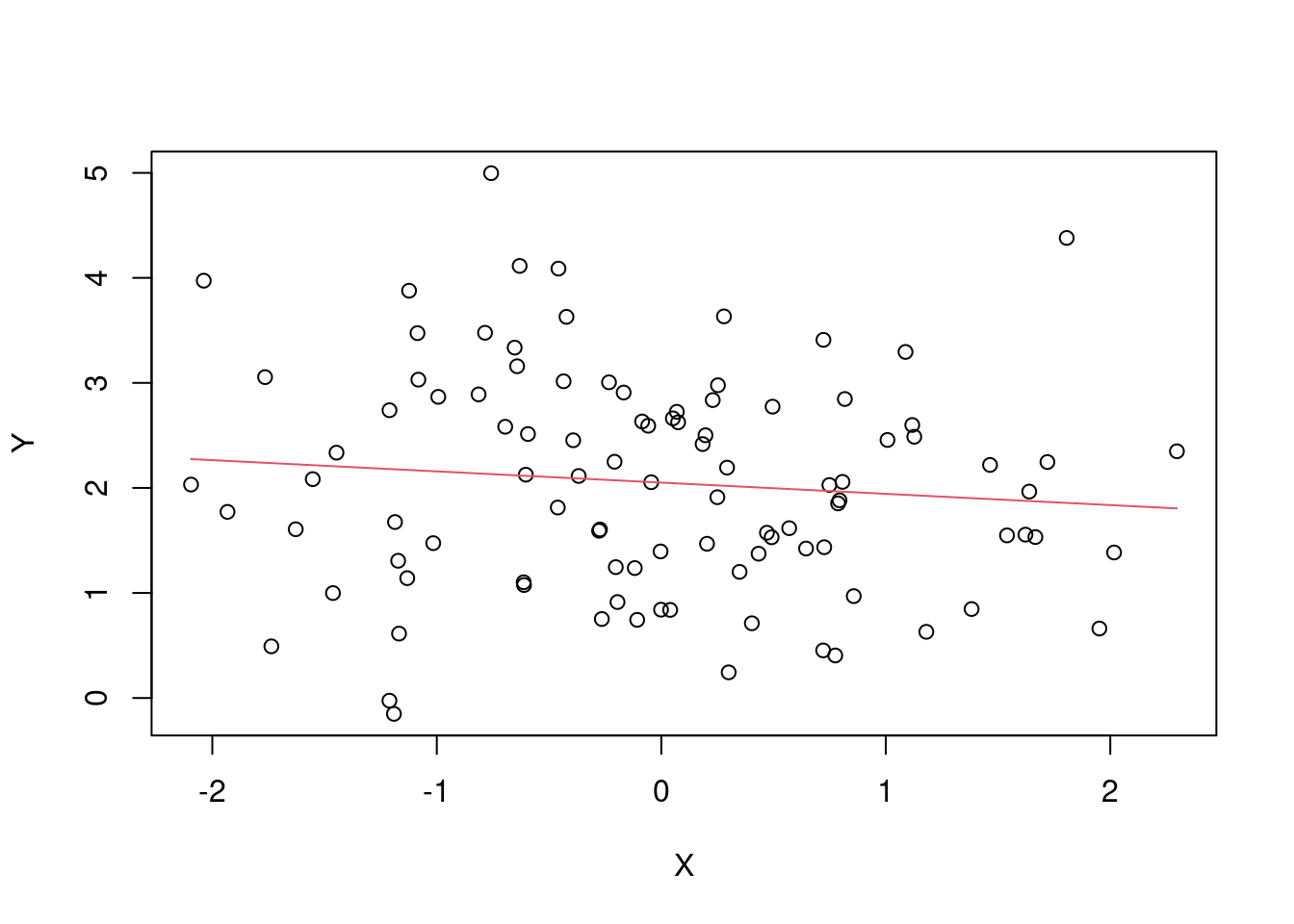
# Estimativa dos erros (resíduos)
residuos = Y-Ypredito
plot(X, Y)
plot(X, residuos)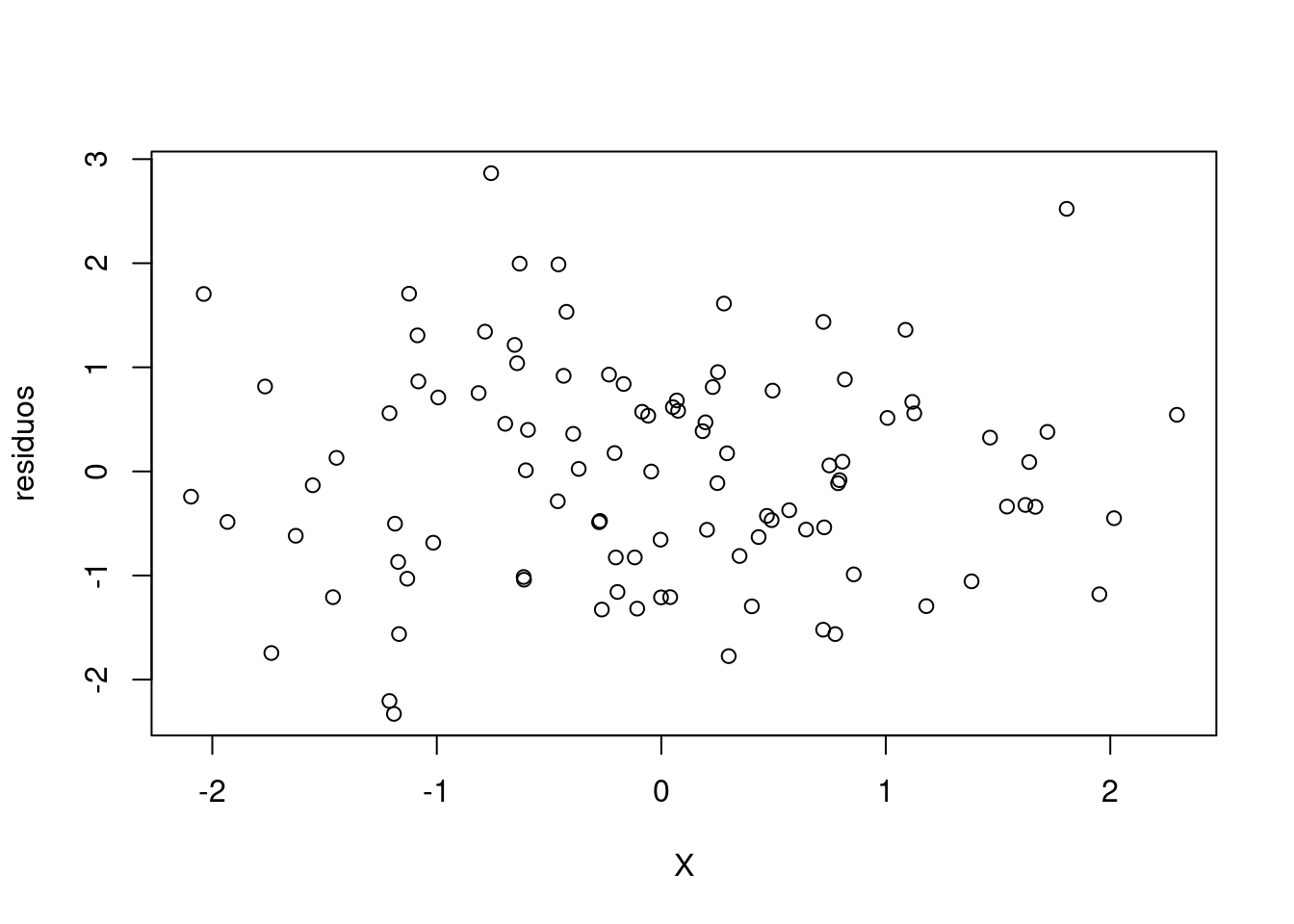
Modelo de regressão linear múltipla:
Objetivo: Prever o valor de Y utilizando múltiplas variáveis. Fazendo um exemplo com 3:
Neste caso, quero achar os betas que melhor se ajustam ao que estou querendo modelar. Note que é uma função linear, quero saber quais são os pesos que me ajudam a ter uma melhor predição.
Estimadores de Mínimos quadrados:
Supondo um exemplo de regressão múltipla com 3 variáveis:
Estimando
N=100
#Simular um modelo linear
X=rnorm(N)
Z=rnorm(N)
W=rnorm(N)
Erro=rnorm(N)
Y= 3 + 5*X + 0*W -2*Z + Erro
#Estimadores de Minimos quadrados para alfa e beta1, beta2 e beta3
#Cria o vetor Ytil (em pe) e a matriz Xmat (Design Matrix)
Ytil=matrix(Y,N,1)
Xmat=matrix(1,N,4)
Xmat[,2]=X
Xmat[,3]=W
Xmat[,4]=Z
#Faz os calculos
betahat= solve(t(Xmat)%*%Xmat)%*%t(Xmat)%*%Ytil
#Estimativa dos erros (residuos)
residuos=Y-YpreditoNo R, utlizamos a função lm para implementação do modelo. Neste caso, explicando Y em função das variáveis independentes X, W e Z:
modelo = lm(Y~X+W+Z)Se comparar os resultados deste com o que foi feito manualmente acima, pode verificar que é idêntico ao que foi calculado manualmente:
summary(modelo)##
## Call:
## lm(formula = Y ~ X + W + Z)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.5372 -0.5787 -0.1411 0.5047 2.7754
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.85185 0.08660 32.930 <2e-16 ***
## X 5.19544 0.08702 59.703 <2e-16 ***
## W 0.06157 0.08877 0.694 0.49
## Z -1.92969 0.09516 -20.278 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8585 on 96 degrees of freedom
## Multiple R-squared: 0.9796, Adjusted R-squared: 0.979
## F-statistic: 1540 on 3 and 96 DF, p-value: < 2.2e-16Olhando a tabela de resultados,
- Estimate = mesmos valores estimados antes
- Std Error: desvio padrão do estimador
- t valor: o valor de t (veremos posteriormente)
- Pr(>|t|): neste modelo se o p-valor for menor que 5%, temos evidências que este valor é estatisticamente diferente de zero
Olhando o resultado do W, você consegue verificar que o valor-p é muito maior, o que de fato, pela nossa construção é possível verificar.
- R2 ajustado corrige pelo número de variáveis que estão sendo utilizadas
- R não ajustado considera todas as variáveis que estão entrando
Modelo polinomial de ordem 3
X = rnorm(100)
Erro = rnorm(100)Seja o polinômio de ordem três: Y = 2 + 3X +0.5X^2 + 0.1*X^3 + Erro
plot(X, Y)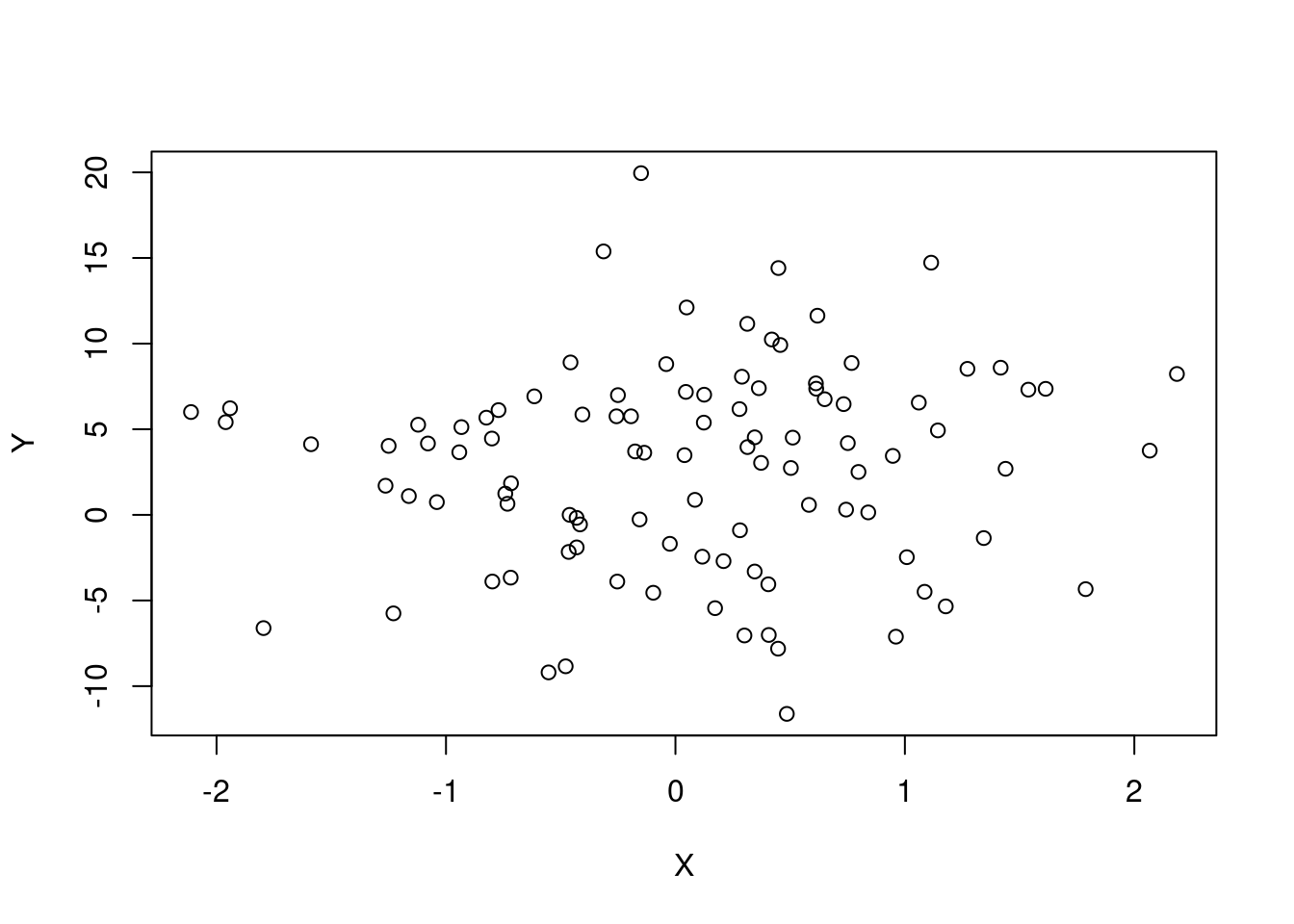
Y=2 + 3*X + 1*X^2 + 0.1* X^3
plot(X, Y)
modelo = lm(Y~X)
lines(X, modelo$fit, col = 2)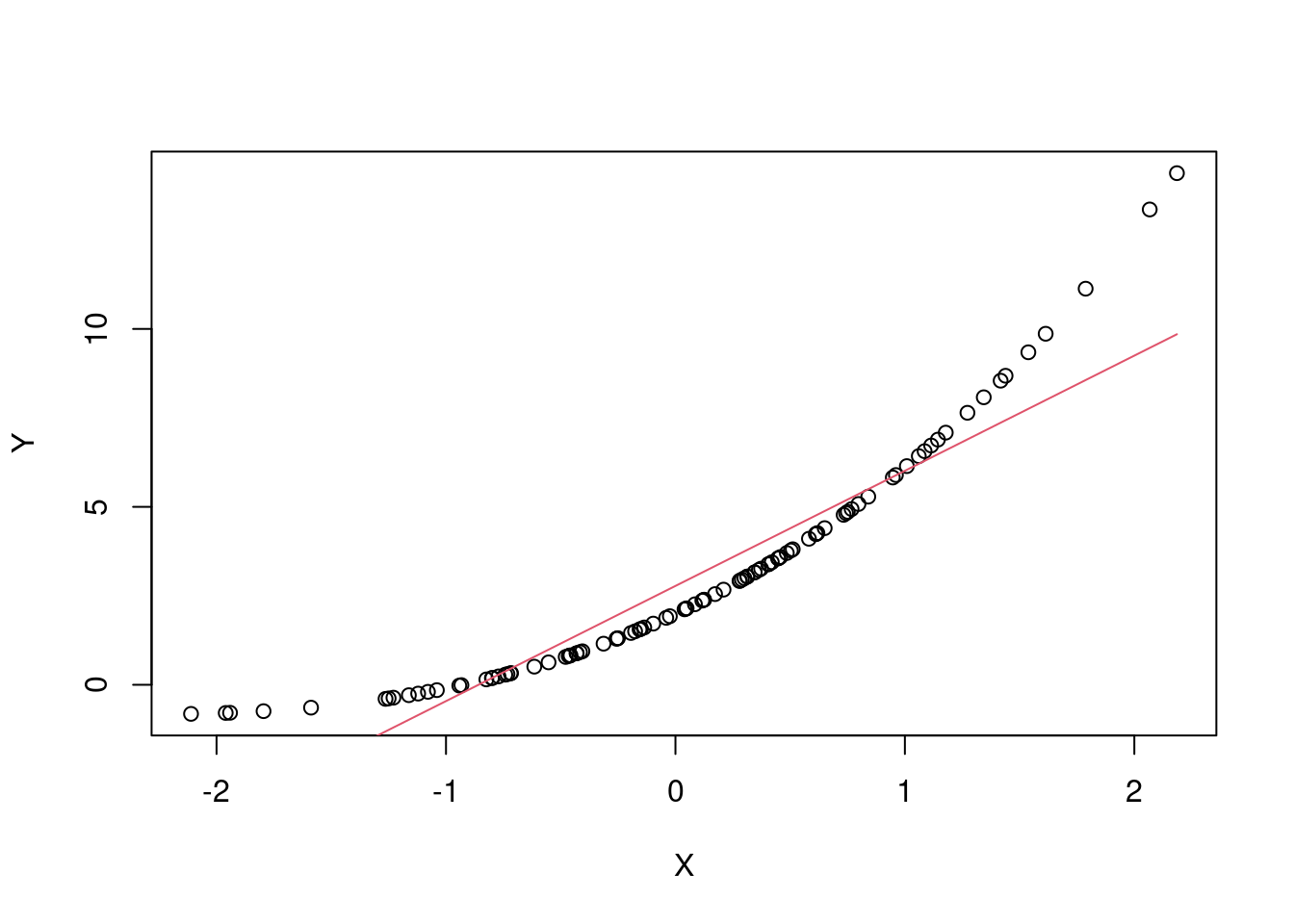
Neste caso é possível verificar que um modelo linear não se adequa diretamente bem, pois trata-se de uma curva. Passamos então a construir com mais variáveis.
Aplicando a regressão lm prevendo Y usando X, W e Z:
# termo quadrático
W = X^2
# termo cúbico:
Z = X^3
Ypredito = modelo$fitSe colocar esse modelo para visualização, podemos ver a seguinte bagunça:
plot(X, Y)
lines(X, Ypredito, col=2)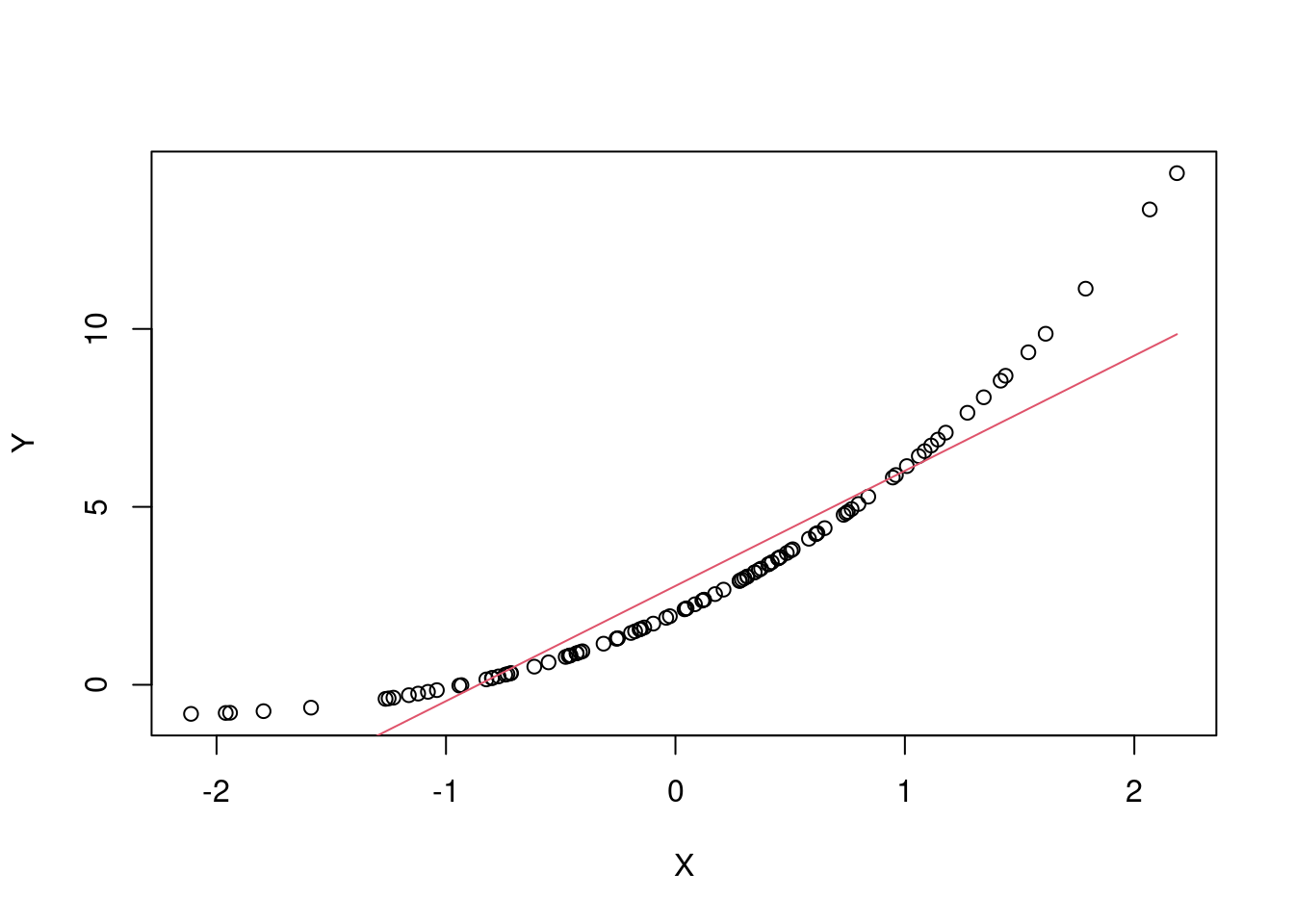
Isso acontece porque ele liga todos os pontos na ordem em que é gerado, o que não é adequado para esse novo modelo. Por isso utilizamos o points:
plot(X, Y)
points(X, Ypredito, col=2)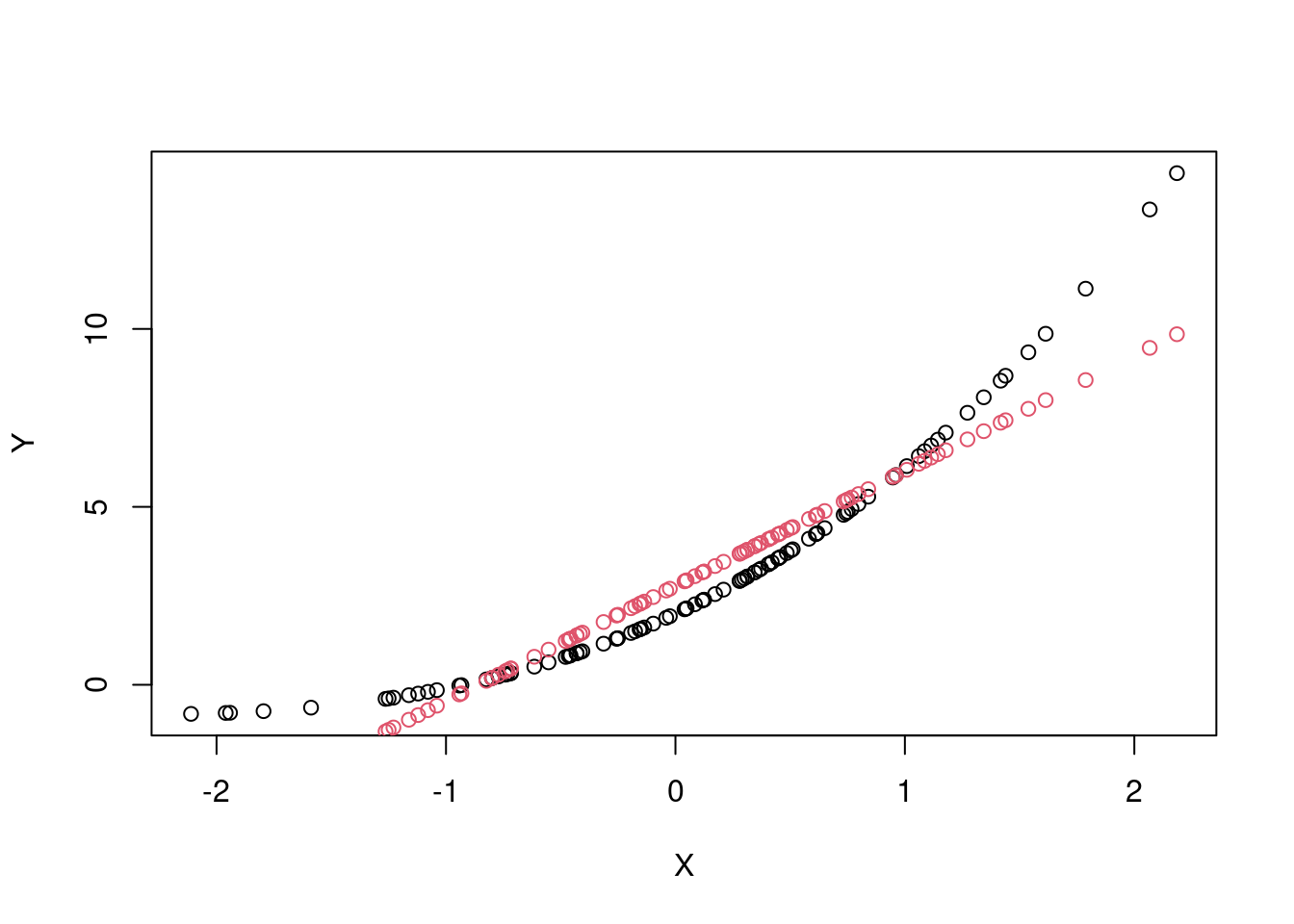
Na próxima aula, veremos mapas probabilísticos para estimar os mapas de ativação do bold. Também é válido para o NIRs.