Análise Espectral
O conteúdo dessa aula auxilia no entendimento da amostragem no domínio da frequência e reconstrução de sinais de tempo discreto. No quesito de análise de dados com EEG, os processos de transformação de amostras do domínio do tempo para o domínio da frequência. Estas incluem tanto a análise direta do espectro de frquência, bem como convoluções. Existem variações relacionadas com a transformada, dependendo do tipo de cada função.
A análise espectral decompõe o sinal de EEG em suas componentes fundamentais (harmônicos) que geram frequências conhecidas que podem ser distinguidas entre si.
O sinal de EEG é composto de várias outras ondas, de modo que a análise espectral consiste em realizar uma decomposição da onda de EEG em diversas ondas senoidais (ou cossenoides). Essa decomposição consiste na aplicação da transformada de Fourier.
A transformada de Fourier converte uma seqüência finita de amostras igualmente espaçadas de uma função em uma seqüência de comprimento igual de amostras igualmente espaçadas da transformada de Fourier em tempo discreto (DTFT), que é uma função de frequência de valor complexo (na literatura poderá conferir que muitas vezes o número imaginário
O intervalo no qual o DTFT é amostrado é recíproco a duração da sequência de entrada. Uma DFT inversa é uma série de Fourier, possuindo os mesmos valores de amostra da seqüência de entrada original. A DFT é, portanto, considerada uma representação do domínio da frequência da sequência de entrada original. Se a sequência original abranger todos os valores diferentes de zero de uma função, seu DTFT é contínuo (e periódico), e o DFT fornece amostras discretas de um ciclo. Se a sequência original é um ciclo de uma função periódica, a DFT fornece todos os valores diferentes de zero de um ciclo de DTFT.
O sinal de EEG de:
Pelas relações trigonométricas:
pode-se representar a decomposição do sinal de EEG como:
T = 100
lambda1 = 30
lambda2 = 50
lambda3 = 110
x= sin(2*pi*lambda1*(1:T)/T) +0.5*sin(2*pi*lambda2*(1:T)/T)
+0.25*sin(2*pi*lambda3*(1:T)/T)## [1] 1.469463e-01 2.377641e-01 2.377641e-01 1.469463e-01 -5.514005e-16
## [6] -1.469463e-01 -2.377641e-01 -2.377641e-01 -1.469463e-01 1.102801e-15
## [11] 1.469463e-01 2.377641e-01 2.377641e-01 1.469463e-01 1.221552e-16
## [16] -1.469463e-01 -2.377641e-01 -2.377641e-01 -1.469463e-01 2.205602e-15
## [21] 1.469463e-01 2.377641e-01 2.377641e-01 1.469463e-01 -9.806459e-16
## [26] -1.469463e-01 -2.377641e-01 -2.377641e-01 -1.469463e-01 -2.443104e-16
## [31] 1.469463e-01 2.377641e-01 2.377641e-01 1.469463e-01 1.469267e-15
## [36] -1.469463e-01 -2.377641e-01 -2.377641e-01 -1.469463e-01 4.411204e-15
## [41] 1.469463e-01 2.377641e-01 2.377641e-01 1.469463e-01 -3.186248e-15
## [46] -1.469463e-01 -2.377641e-01 -2.377641e-01 -1.469463e-01 1.961292e-15
## [51] 1.469463e-01 2.377641e-01 2.377641e-01 1.469463e-01 -7.363355e-16
## [56] -1.469463e-01 -2.377641e-01 -2.377641e-01 -1.469463e-01 -4.886208e-16
## [61] 1.469463e-01 2.377641e-01 2.377641e-01 1.469463e-01 1.713577e-15
## [66] -1.469463e-01 -2.377641e-01 -2.377641e-01 -1.469463e-01 -2.938533e-15
## [71] 1.469463e-01 2.377641e-01 2.377641e-01 1.469463e-01 -1.004737e-14
## [76] -1.469463e-01 -2.377641e-01 -2.377641e-01 -1.469463e-01 8.822409e-15
## [81] 1.469463e-01 2.377641e-01 2.377641e-01 1.469463e-01 -7.597453e-15
## [86] -1.469463e-01 -2.377641e-01 -2.377641e-01 -1.469463e-01 6.372496e-15
## [91] 1.469463e-01 2.377641e-01 2.377641e-01 1.469463e-01 -5.147540e-15
## [96] -1.469463e-01 -2.377641e-01 -2.377641e-01 -1.469463e-01 3.922584e-15ts.plot(x)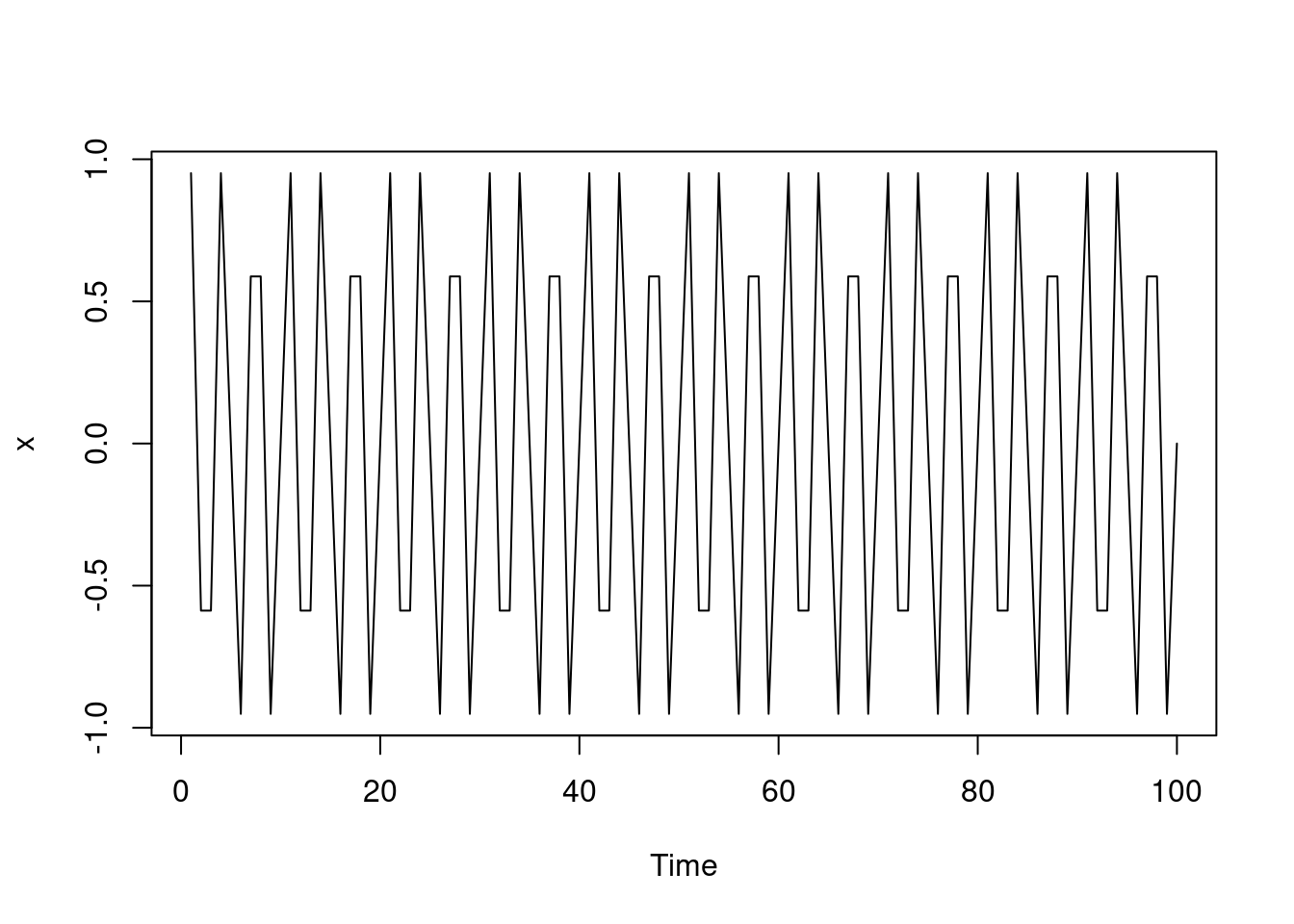
Ruído-branco Gaussiano é um sinal aleatório com igual intensidade em diferentes frequências, o que lhe dá uma densidade espectral de potência constante. Em termos discretos, é um sinal discreto cujas amostras são vistas como uma seqüência de variáveis aleatórias não autocorrelacionadas com média zero e variância finita. Para calcular o espectro, utiliza-se a transformada de Fourier: A Transformada rápida de Fourier (em inglês fast Fourier transform, ou FFT) é um algoritmo eficiente para se calcular a Transformada discreta de Fourier (DFT) e a sua inversa. A análise de Fourier converte um sinal do seu domínio original para uma representação no domínio da frequência e vice-versa. Idêntico à definição se T for potência de 2 (ou aproximação de).
A função spectrum realiza a estimativa da densidade espectral de uma série temporal.
hist(rnorm(T))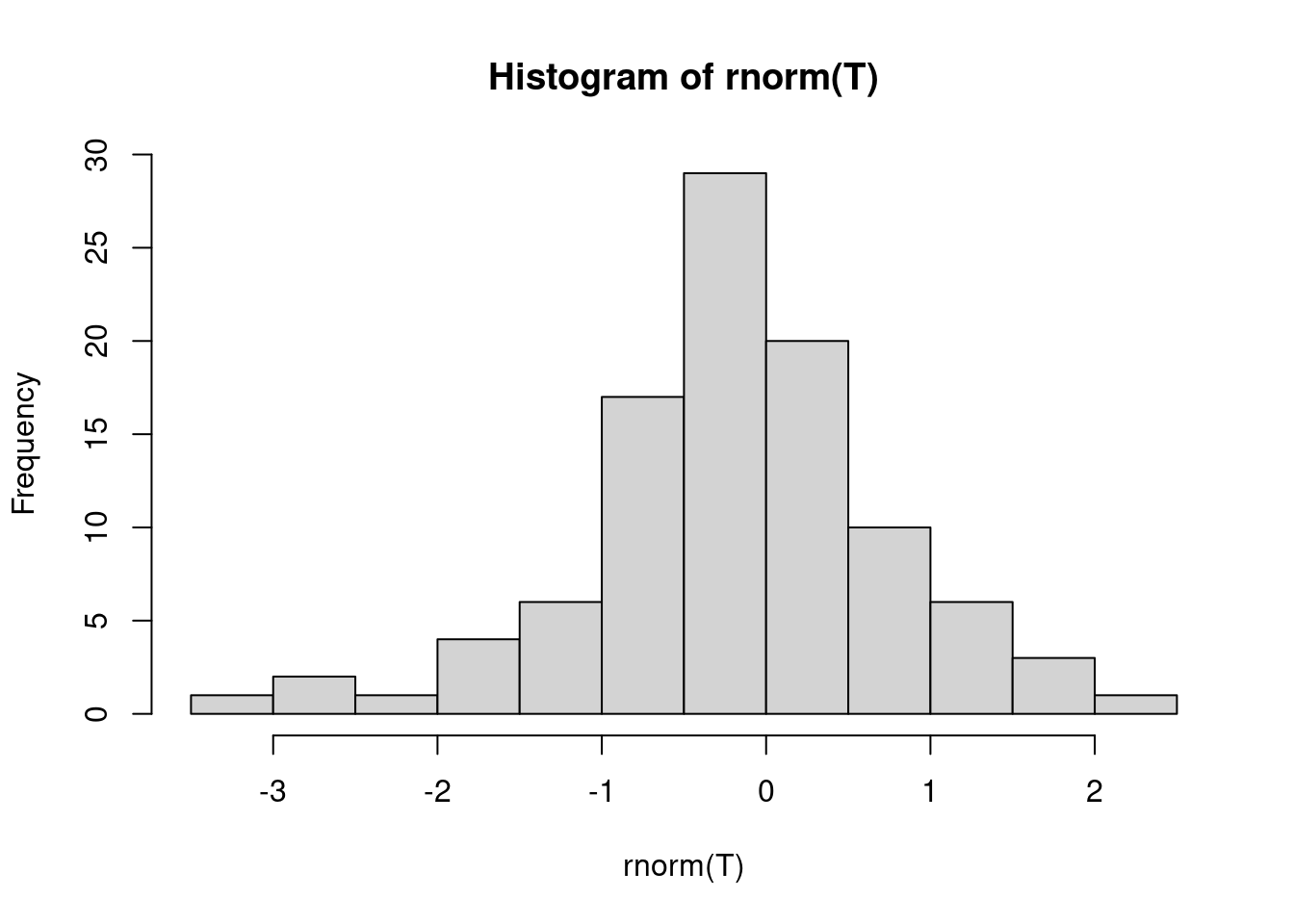
x = x+rnorm(T)
ts.plot(x)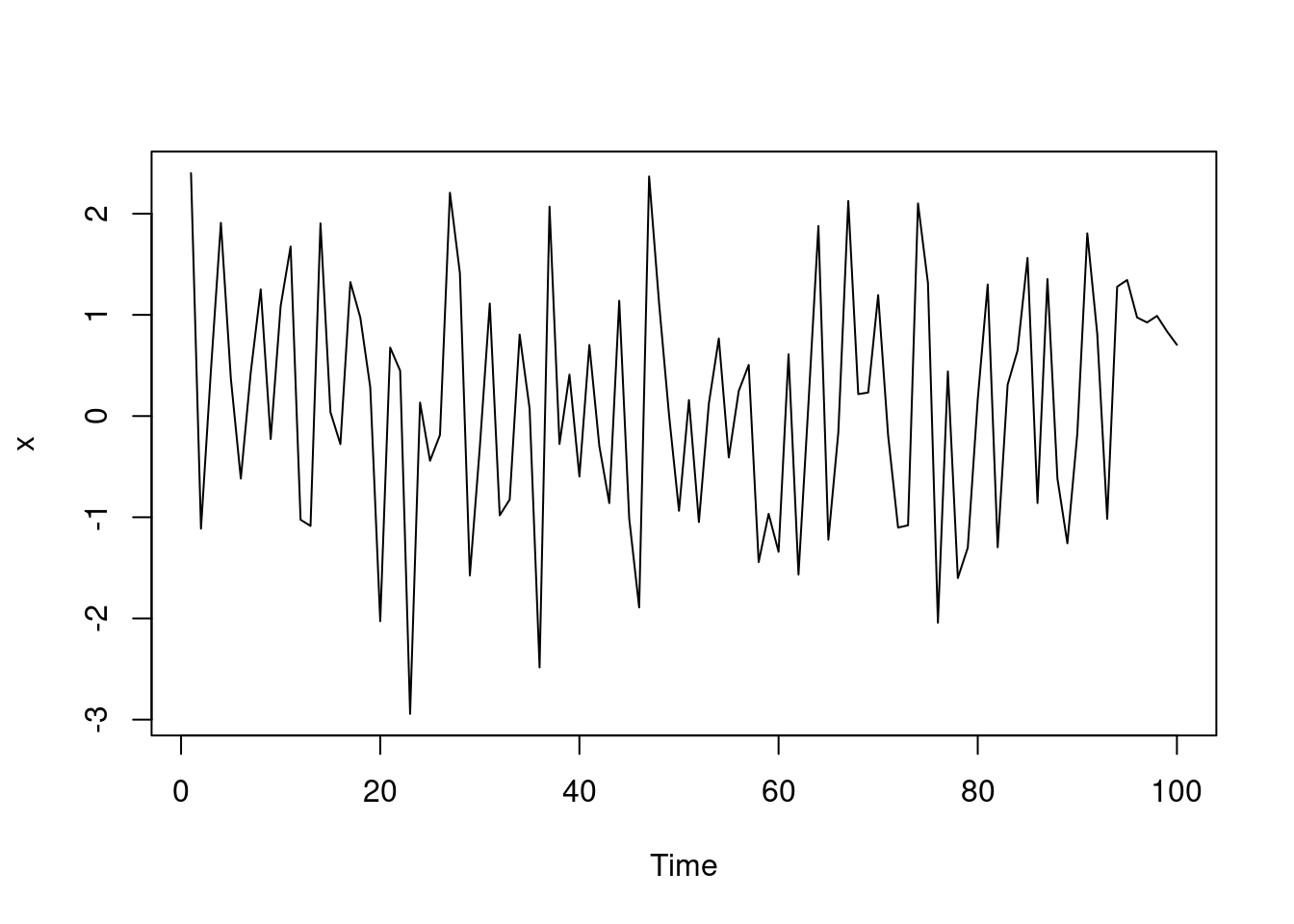
A função spectrum realiza a estimativa da densidade espectral de uma série temporal. O estimador do espectro (periodograma) é definido como “estimado” pois ele faz uma estimativa e não uma média de todos os dados gerados.
Essa análise espectral verifica o valor da amplitude da onda para cada frequência de Fourier. Em EEG, existe um grupo de faixas de frequências que aparecem em situações especificas e a análise espectral permite visualizar o comportamento da amplitude das ondas de EEG para cada um desses grupos, de acordo com o objetivo do estudo, identificando as bandas de frequências:
- Delta <4z
- Teta 4-7hz
- Alfa 8-12hz
- Beta 13-30hz
- Gama > 30hz
O periodograma no R, gráfico com as frequências é determinado por:
ESPECTRO = spectrum(x)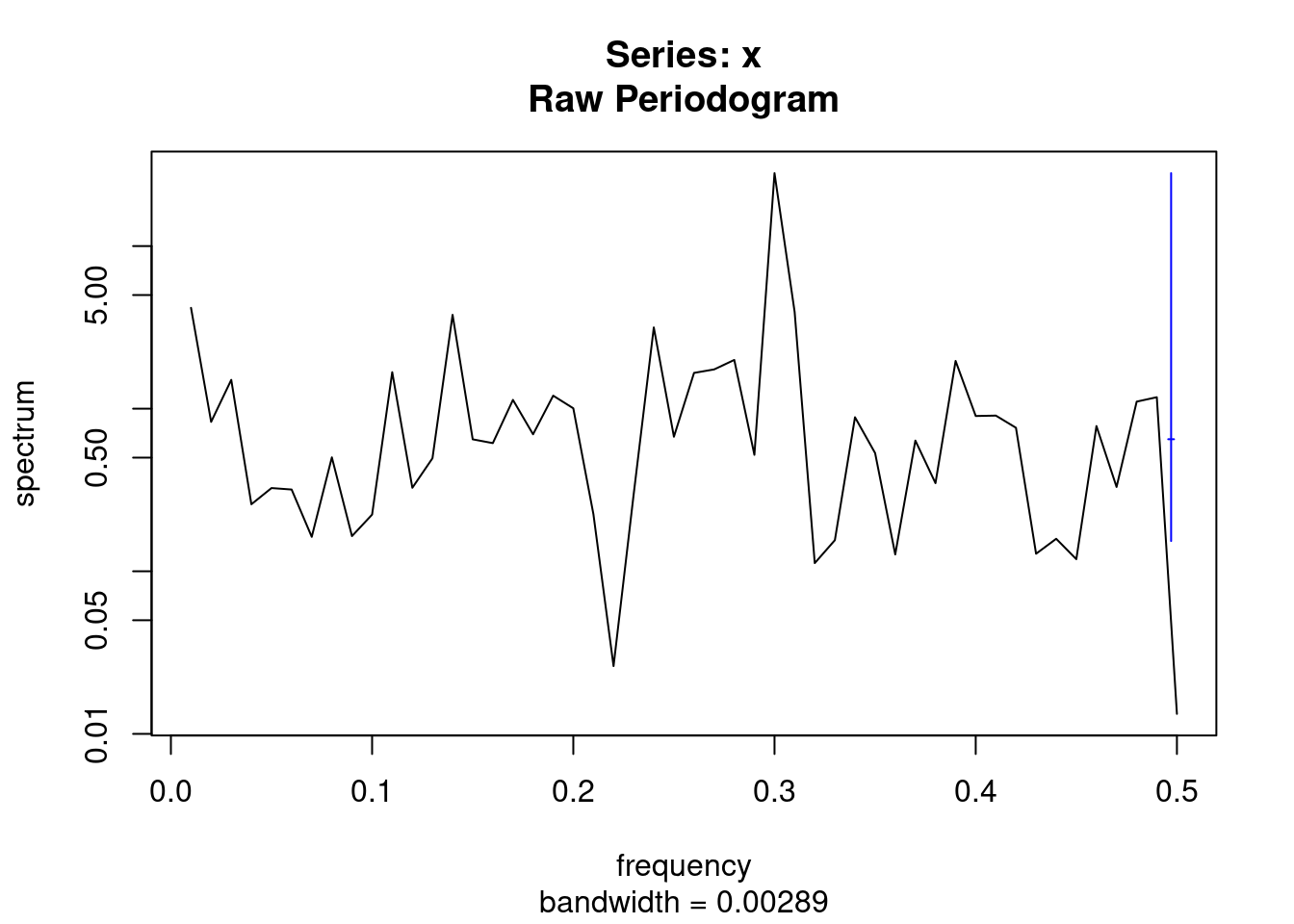
# O eixo x ficaria em
plot(ESPECTRO$freq, ESPECTRO$spec, type = "l")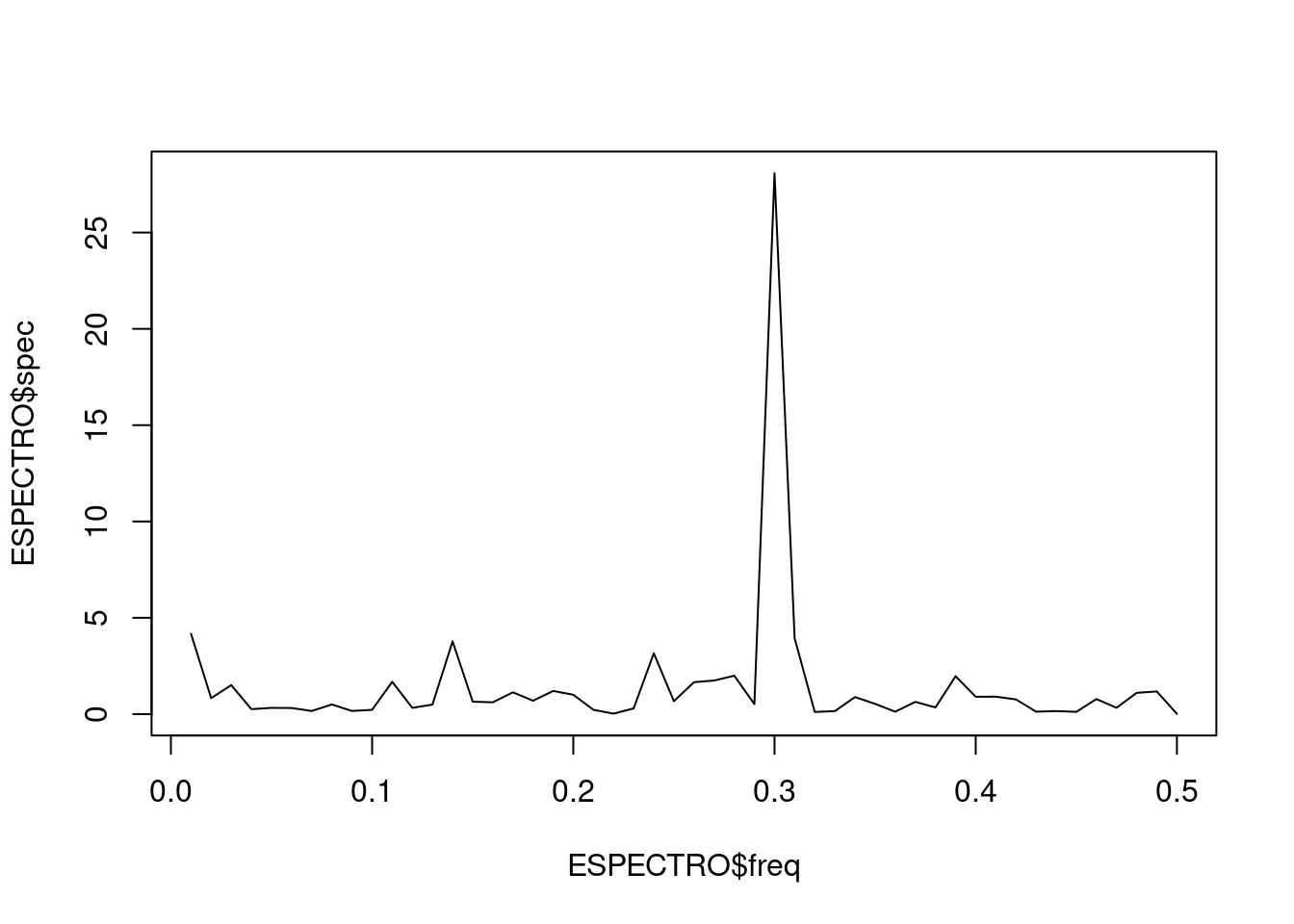
Implementando com o banco de dados
Realizando a leitura dos dados:
#leitura dos sinais
sinais=read.table("./data/OlhosFechados.txt",header=FALSE)
#leitura do nome dos canais
nomescanais=scan("./data/NOMEScanais.txt",what="string")
dim(sinais)## [1] 45315 32nomescanais ## [1] "Fp1" "Fp2" "F7" "F3" "Fz" "F4" "F8" "FC5" "FC1" "FC2"
## [11] "FC6" "T7" "C3" "Cz" "C4" "T8" "TP9" "CP5" "CP1" "CP2"
## [21] "CP6" "TP10" "P7" "P3" "Pz" "P4" "P8" "PO9" "O1" "Oz"
## [31] "O2" "PO10"Parametrizando as variáveis iniciais:
#Taxa de amostragem
HZ=250
#Tamanho da epoca (janela) em segundos
TAMsegundos=5
#Tamanho da epoca (janela) em caselas do vetor de sinais
TAM=TAMsegundos*HZ
#Numero de epocas
Nepocas=floor(nrow(sinais)/TAM)
#Numero de canais
Ncanais=ncol(sinais)Criando matriz Espectro para armazenar a média dos periodogramas entre todas as épocas para cada canal. As linhas representam diferentes frequências As colunas representam os canais
ESPECTRO=matrix(0,TAM/2,Ncanais)
#Calcular para cada canal
# Escondi a saída de todos os espectros porque tem muitos canais e épocas na saída
for(canal in 1:Ncanais){
y=0
#Calcula a media entre épocas
for(epoca in 1:Nepocas){
#Descobrir caselas de inicio e fim de cada epoca
INICIO=TAM*(epoca-1)+1
FIM=epoca*TAM
y=y+spectrum(sinais[INICIO:FIM,canal], plot = FALSE)$spec
}#for da epoca
ESPECTRO[,canal]=y/Nepocas
}#for do canalGráfico do espectro no canal O1, coluna 29.
plot((HZ/2)*(1:nrow(ESPECTRO))/nrow(ESPECTRO), ESPECTRO[, 29],
type="l", xlab="Frequencia (Hz)", ylab="Potencia (uV^2)")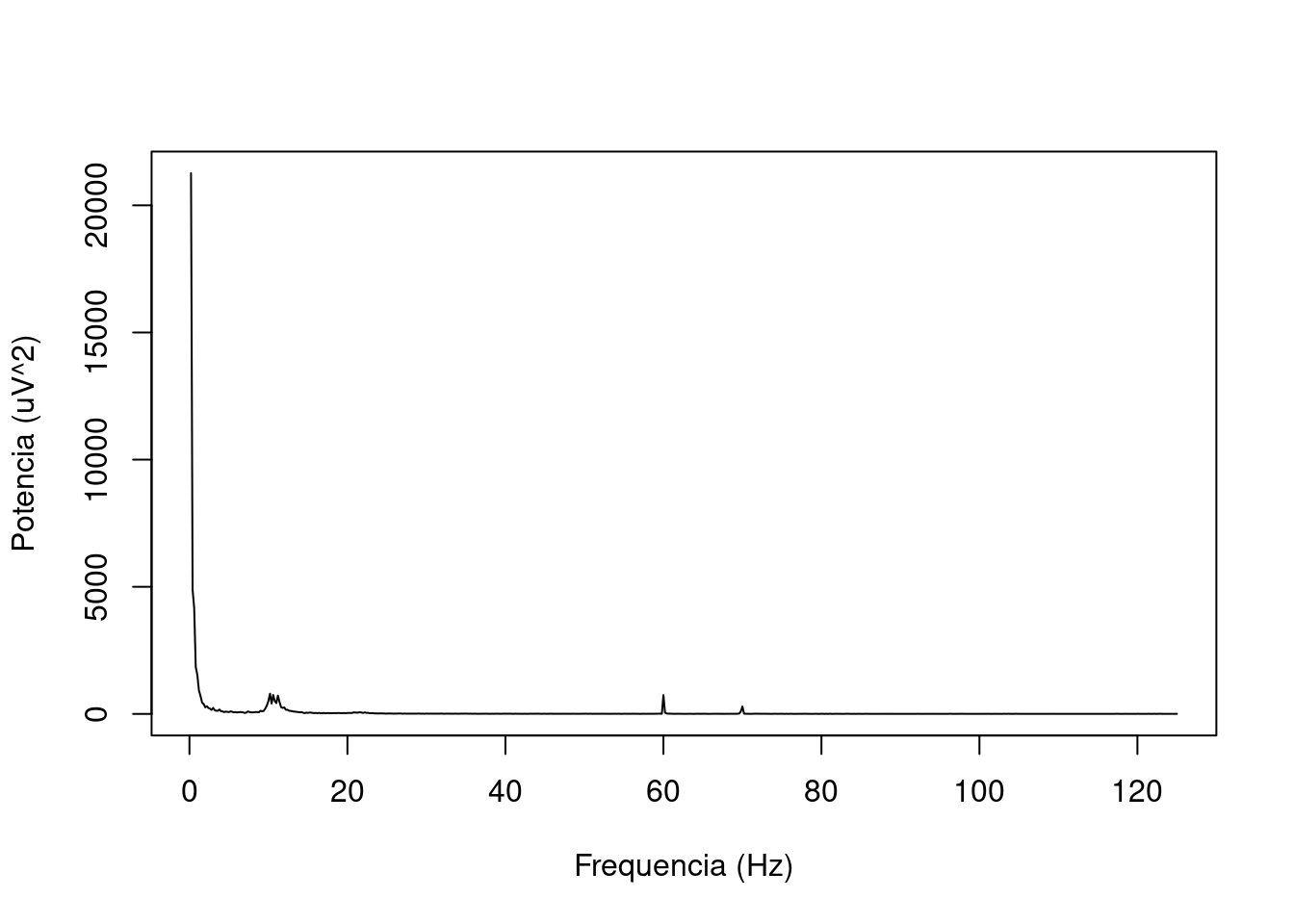
Ajustando o zoom para conseguir visualizar a informação melhor:
IX=10:200
plot((HZ/2)*IX/nrow(ESPECTRO), ESPECTRO[IX,29],
type="l",xlab="Frequencia (Hz)",ylab="Potencia (uV^2)")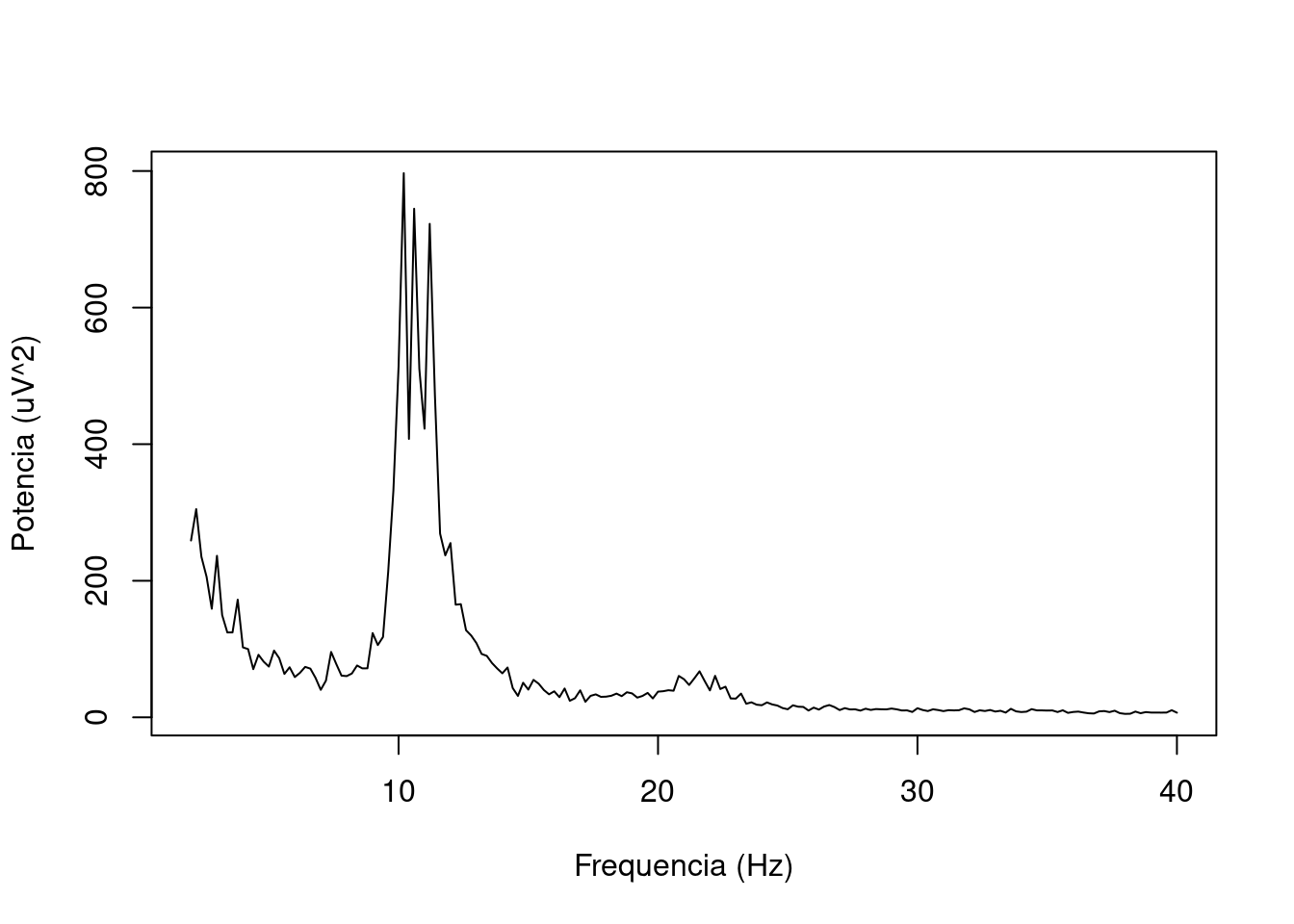
#Armazenar o espectro estimado médio de olhos fechados
ESPECTROof=ESPECTROPara armazenar o espectro estimado médio de olhos abertos e colocar os dois no mesmo gráfico:
ESPECTROoa=ESPECTRO
##### COLOCAR OS 2 espectros médios no mesmo grafico
#ZOOM no grafico
IX=10:200
plot((HZ/2)*IX/nrow(ESPECTROof), ESPECTROof[IX,29],
type="l",xlab="Frequencia (Hz)",ylab="Potencia (uV^2)")
legend("topright",c("Olhos Fechados","Olhos Abertos"),lty=c(1,1),
col=c(1,2))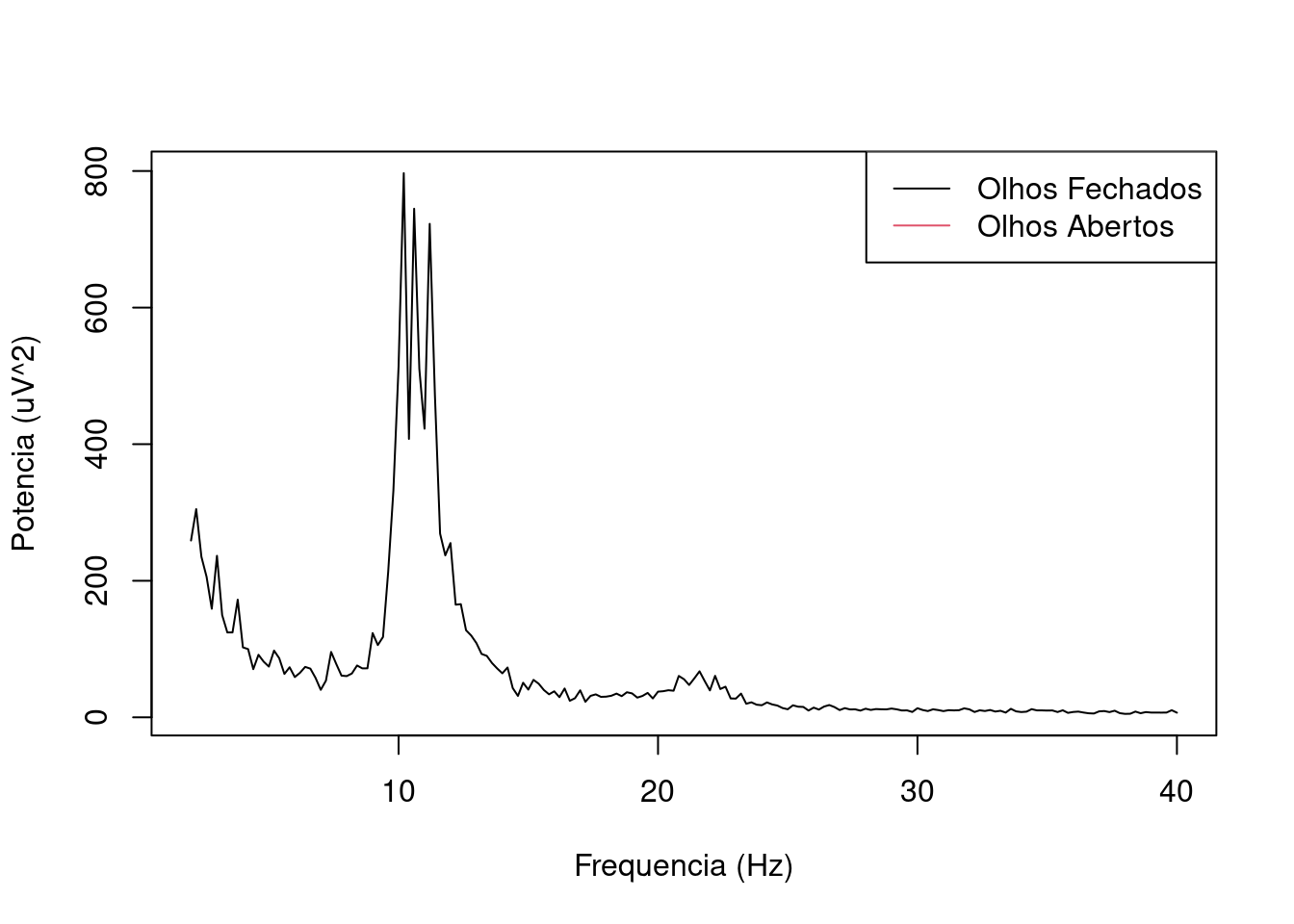
No gráfico podemos o espectro para cada frequência (analisar o espectro para cada faixa) e não a evolução em si (pois não está no tempo).