Filtros de sinais
O processo de filtragem de sinais permite a caracterização dos sinais a partir de suas características. Por exemplo, aplicado ao som as frequências mais altas representam os sons mais agudos, enquanto que as frequências mais baixas representam os sons mais graves.
Os artefatos em EEG caracterizam de ondas não cerebrais, denominadas por ruídos, como por exemplo a frequência da rede elétrica de 60hz, ondas de baixas frequências devido ao calor no couro cabeludo do indivíduo. Deste modo, é extremamente importante aplicação de filtros nestes sinais para remoção de tais artefatos antes de qualquer outra análise.
Para tratar esses sinais, seja, frequências altas, baixas ou algum determinado intervalo, definimos um filtro passa baixa a partir da subtração do sinal original pela média aritmética dos pontos ao redor. Alguns conceitos importantes para a construção dos filtros:
- Frequência de amostragem: Trata-se da frequência de sinais observados em um intervalo de tempo (medidos em hertz = 1/s).
- Ex: No EEG utiliza-se uma frequência de 250 por segundo. Com FNIRS, utiliza-se em torno de 7 frames por segundo. Na ressonância magnética funcional (fMRI), temos 1 imagem a cada 2 segundos. Logo, a frequência de amostragem é 1/2 = 0.5Hz
- Observação: A frequência = 1/período da observação
- Frequência de Nyquist: Corresponde à metade da frequência da taxa amostragem. Pelo teorema de Nyquist, para prevenir o aliasing (sobreposição de sinais) deve-se:aumentar da taxa de amostragem até duas vezes da maior frequência do sinal. Se o sinal é limitado no tempo a frequência de amostragem deve ser tão alta quanto se conseguir, pois em frequência o sinal se espalha por todo o espectro sendo não limitado; com isso deve-se remover ou filtrar as frequências acima da frequência mais alta desejada evitando a formação do aliasing
- Note: A frequência de Nyquist vale para qualquer modalidade de técnica de neuroiumagem (fMRI,EEG,fNIRS…).
O filtro permite a passagem o sinal de parte dos dados e impede a retirada de outros. São os filtros:
Passa-alta (High pass): Deixa passar as altas frequências (maior importância pra alta frequência e baixa importáncia para baixa frequência.
Passa-baixa (Low pass): Deixa passar as baixas frequências e dá pouca importância às altas frequências.
Passa-banda (band pass): O sinal resultante após o filtro possui apenas a banda de frequência utilizada no filtro.
Implementação de filtros em R e carregando dados:
No R faremos primeiro o desenho do filtro: ou seja definir qual o tipo de frequências vamos passar, para isso usaremos o comando “butter” no pacote signal.
Caso não tenha o pacote, utilize os comandos:
Instalando pacote de sinais no R: * install.packages(“signal”)
e no código chamar a blbioteca
require(signal)O exercício da aula mostra a leitura de um banco de dados de sinais de EEG.
Para isso, será necessário realizar a leitura dos dados:
sinais=read.table("./data/oddball250hz.txt",header=FALSE)ver também a verificação dos dados:
dim(sinais)## [1] 45461 33Olhando o arquivo, ele é composto por 45461 linhas e 33 colunas (essas referentes aos 32 canais e uma última coluna de zeros).
Para verificar os dados do arquivo em um plot:
# Plot da série temporal:
#gambiarra para o ts.plot funcionar no R Studio:
graphics.off()
par("mar")## [1] 5.1 4.1 4.1 2.1par(mar=c(1,1,1,1))e o plot:
# Plotando gráfico de linha
ts.plot(sinais)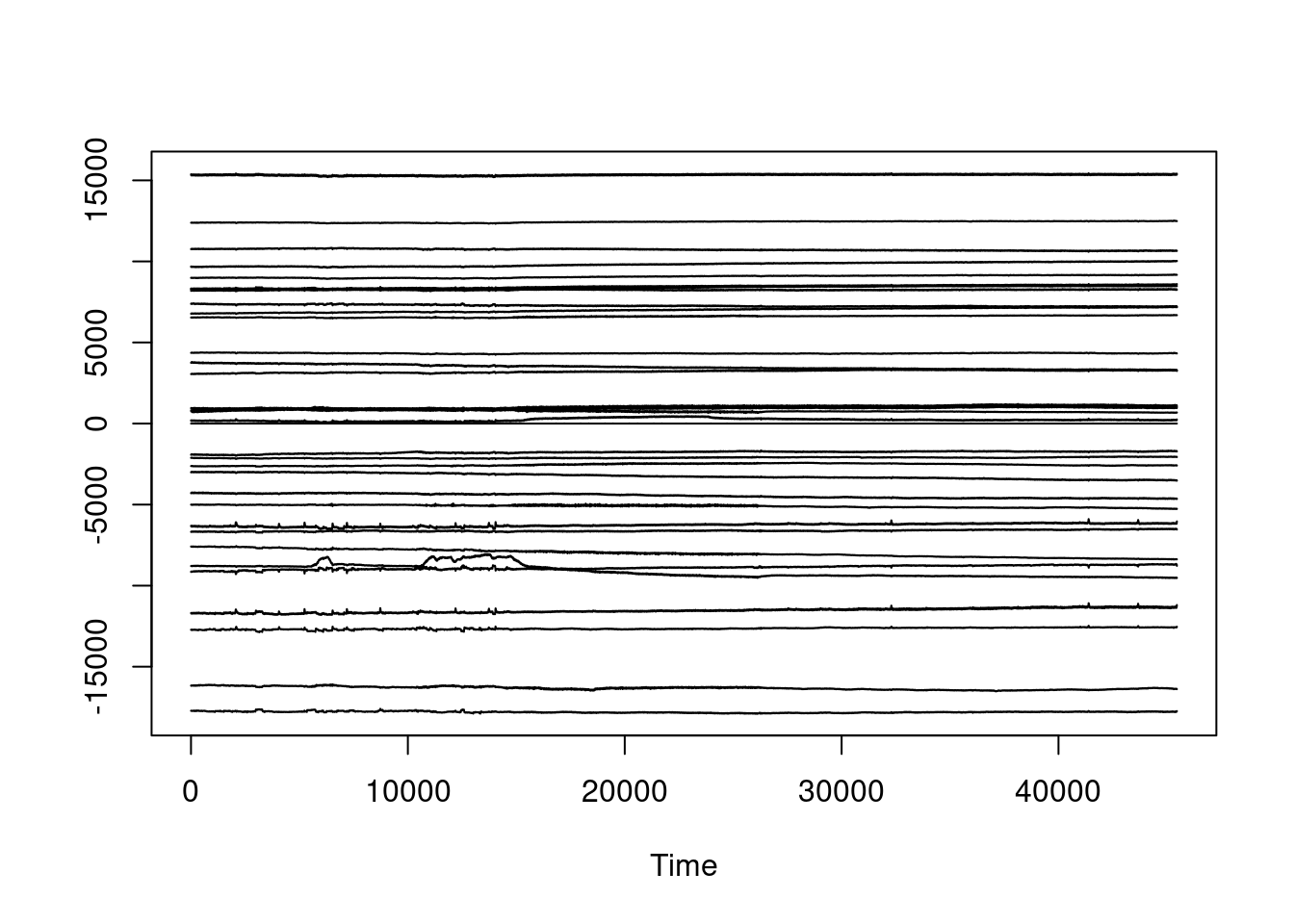
A taxa de amostragem é a frequência em que a leitura ocorre: * HZ=1/INTERVALO, onde 1hz = 1/s
# Suponha que o sinal foi adquirido sob uma taxa de amostragem de 250Hz:
HZ= 250Dessa forma, analisamos o sinal com base nessa amostragem, para todas as linhas, para o canal 5, com o plot do tipo l (linha):
#Fazer gráfico com frescura:
# plot(1:nrow(sinais), sinais[,5],type="l")
# mas preciso considerar a frequência convertendo pra segundos:
plot((1:nrow(sinais))/HZ, sinais[,5], type="l", xlab="Tempo(s)", ylab= "sinal uV")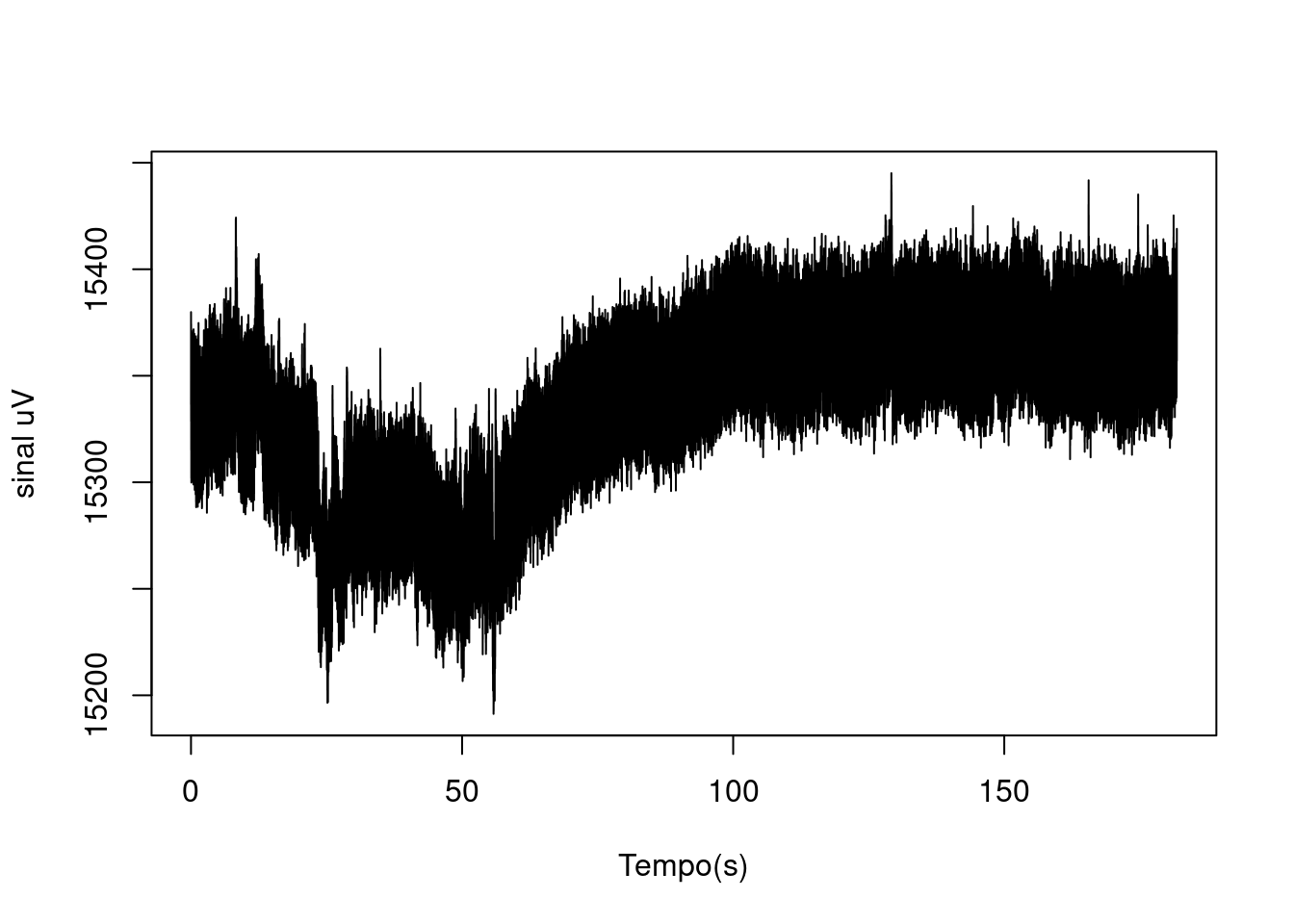
Utilizando a função do filtro (butter):
Primeiramente se define qual o tipo de frequências vamos passar, para isso usaremos o comando “butter”. A função butter possui a seguinte síntaxe: * butter (n = ordem do filtro, w = cutoff, tipo = tipo de filtro) onde, + ordem do filtro = controla o decaimento da curva de ajuste do filtro, geralmente se usa 3 ou 5. + cutoff = frequências que se queira cortar (é um número de 0 a 1, neste caso é preciso fazer uma regra de 3; 0 = 1 e 1= frequências de Nyquist) + type = tipo de filtro (low/passa-baixa, high/passa-alta ou band-pass/passa banda)
Aplicando passa-baixa em 30Hz:
FILTRO = butter(n=5, W =30/(HZ/2), type = "low")
# Gráfico do desenho do filtro:
freqz(FILTRO)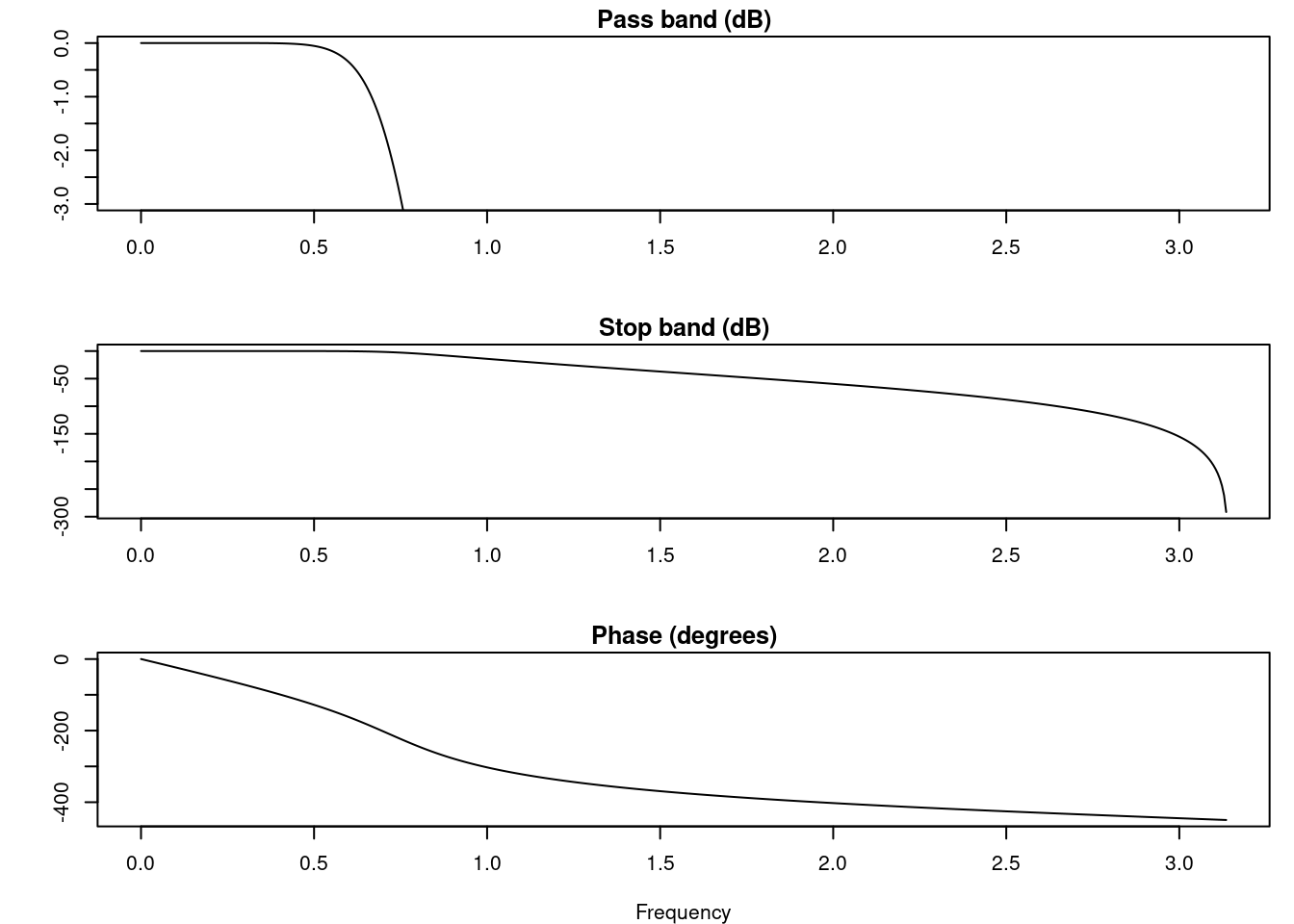
Após ter o filtro desenhado, aplica-lo sobre os dados do canal (neste caso seria o canal 5, como exemplo, mas poderia ser qlq um). Ao aplicar o filtro de forma direta teríamos ainda um problema:
filtrado_teste = filter(FILTRO, sinais[,5])
# bug de início do sinal, com valor muito alto.Neste caso “bugado” teríamos o seguinte retorno:
#Fazer o grafico com os 2 sinais
plot((1:nrow(sinais))/HZ, sinais[,5],type="l",
xlab="Tempo(s)", ylab="sinal(uV)")
#Acrescentar linha com o sinal filtrado
lines((1:nrow(sinais))/HZ, filtrado_teste, col=2)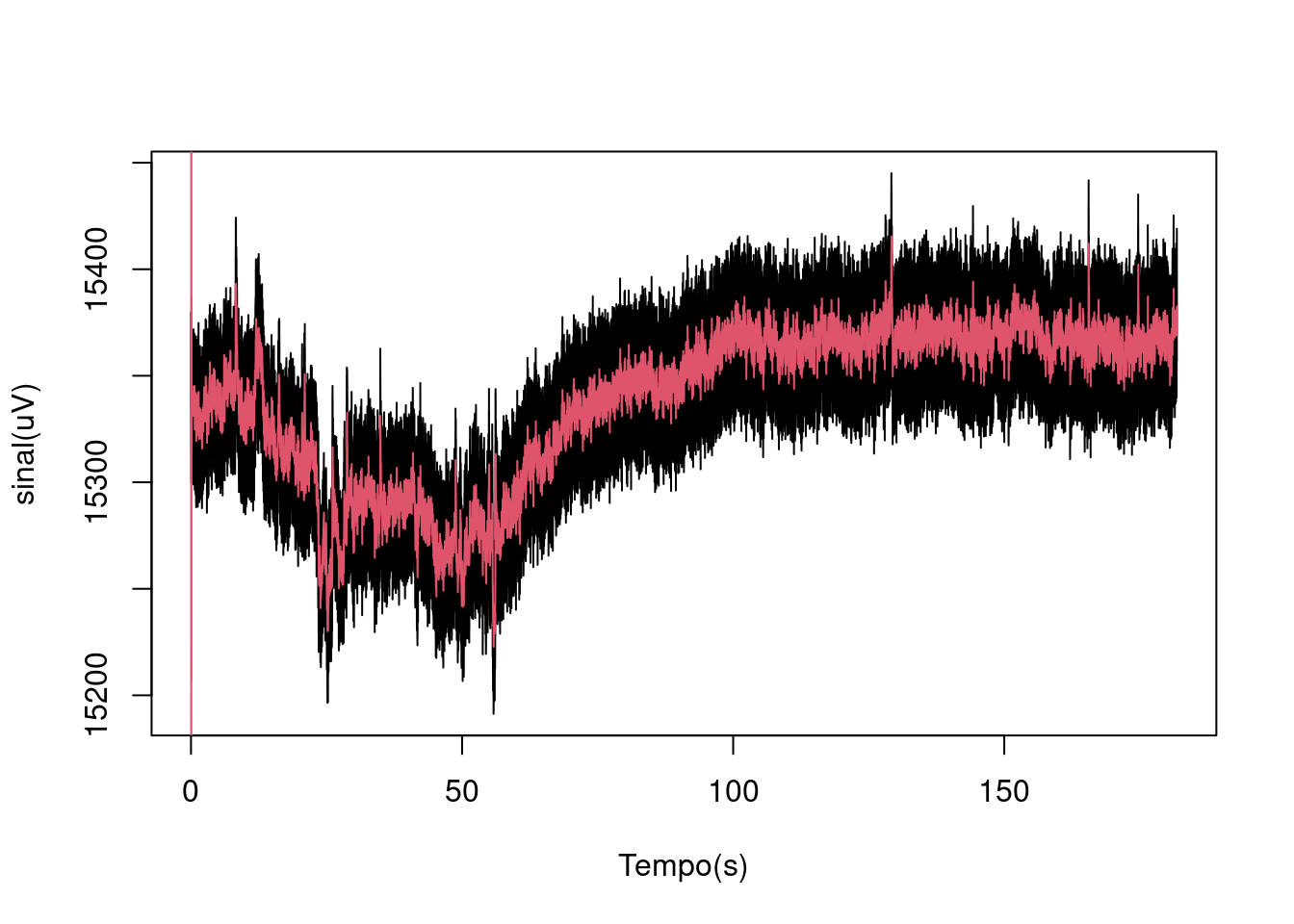
Para isso resolve-se tirando a média do sinal:
y = sinais[,5] - mean(sinais[,5])
# e novamente aplicando o filtro no sinal:
filtrado = filter(FILTRO, y)obtendo então o sinal filtrado:
#Acrescentar linha com o sinal filtrado
plot((1:nrow(sinais))/HZ,y,type="l",
xlab="Tempo(s)", ylab="sinal(uV)")
lines((1:nrow(sinais))/HZ, filtrado, col=2)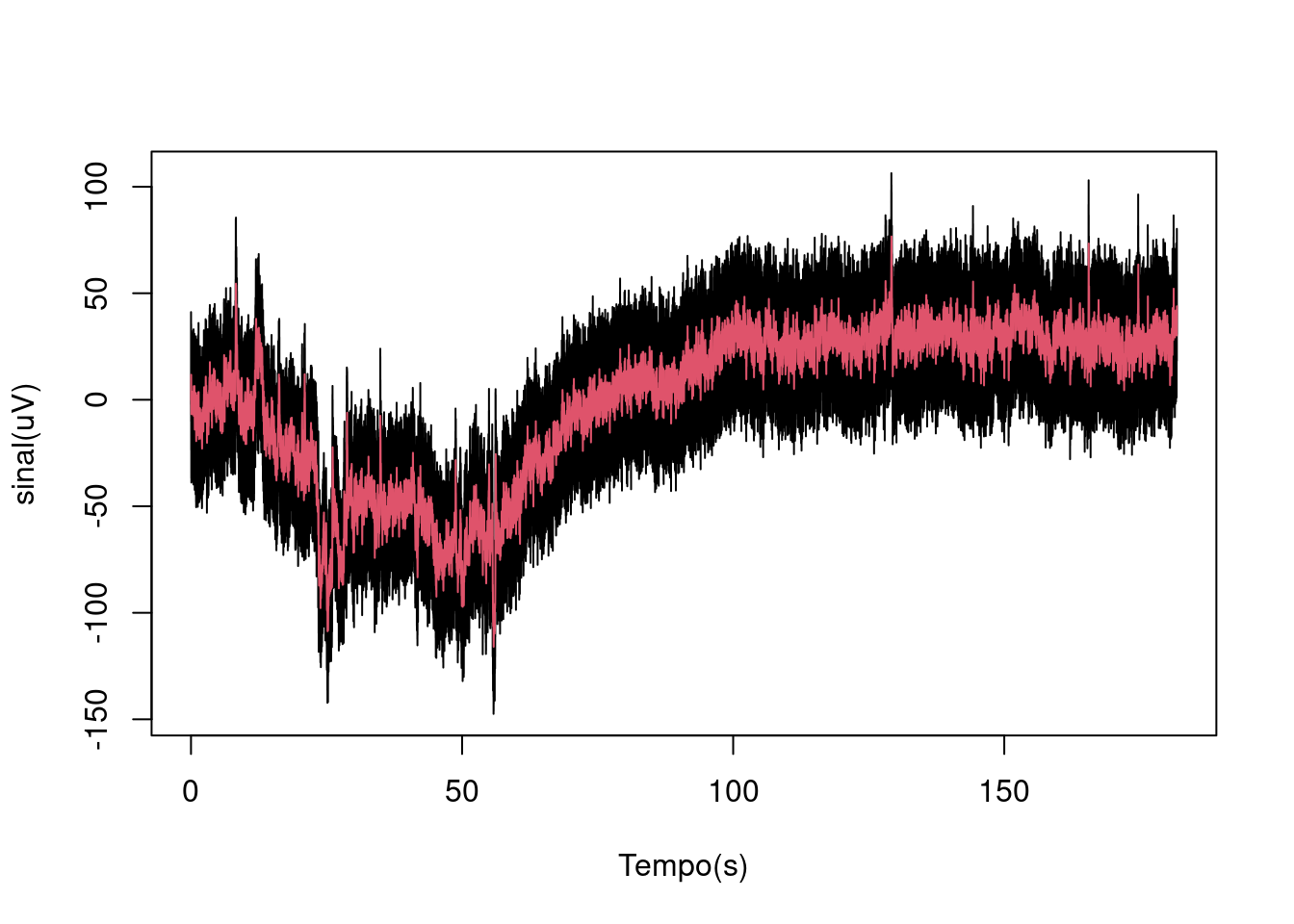
Dessa forma é possível aplicar outros filtros, alterando o tipo na função butter e aplicando aos sinais de todos os canais na função filter. Dica de exercício: Tente executar para outros canais ou então ajustando o filtro para outras frequências ou determinados intervalos de frequência.
Um exemplo comum é a aplicação de um filtro que processe dados de um determinado intervalo (por exemplo, como a rede elétrica é 60hz mas há oscilações, processa-se sinal entre 59-61hz). Neste caso, queremos um passa-banda para deixar apenas entre as frequências de 1-40 hz:
# butter (n = ordem do filtro, w = cutoff, tipo = tipo de filtro)
# - n = Ordem do filtro = controla o decaimento da curva de ajuste do filtro, # geralmente se usa 3 ou 5.
# -type = tipo de filtro (low/passa-baixa, high/passa-alta ou band-pass/passa banda)
FILTRO = butter(n=5, W =c(1,40)/(HZ/2), type = "pass")
freqz(FILTRO)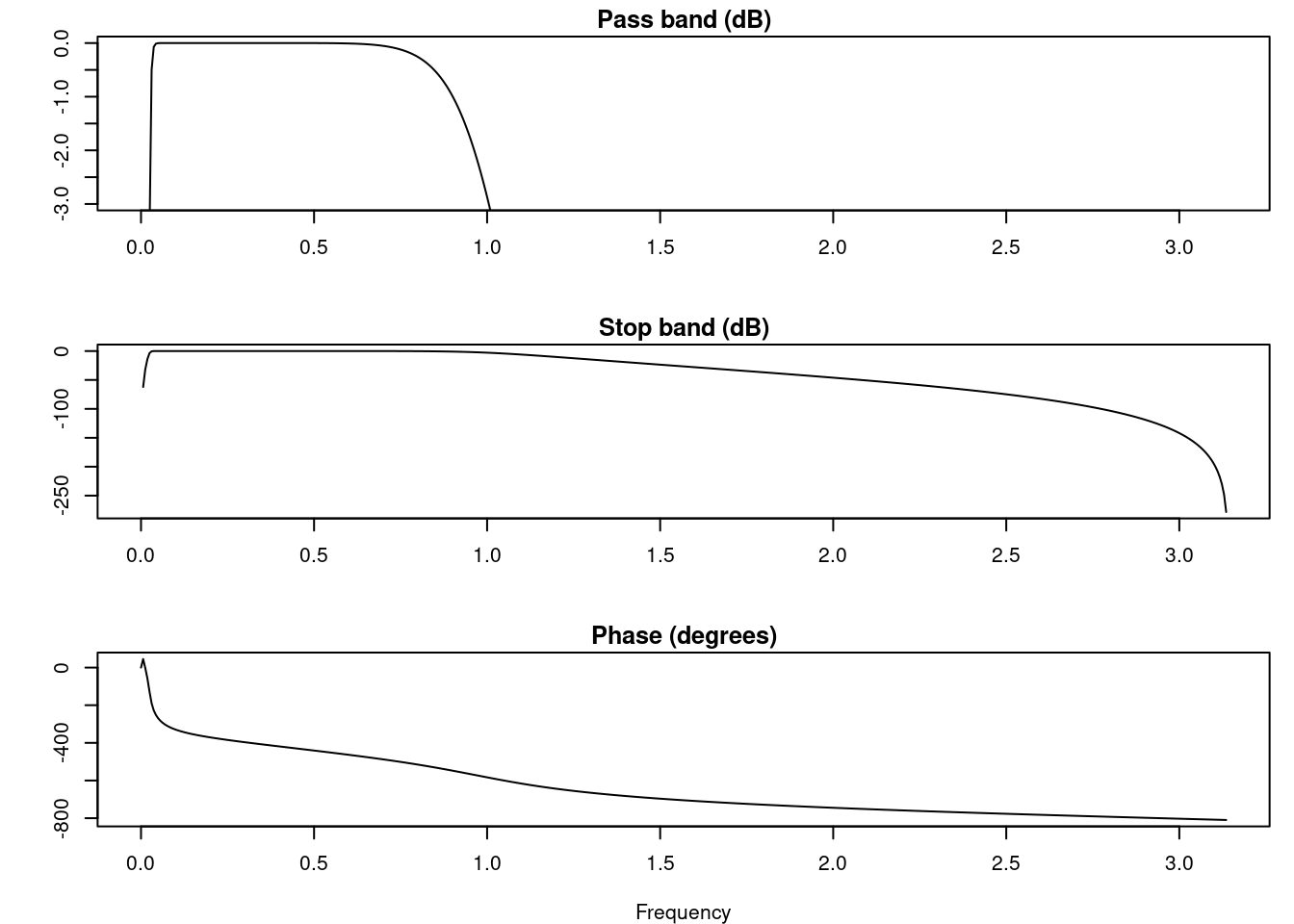
Quero aplicar este filtro em todas as colunas da matriz de sinais, realizando a retirada da média para tirar os outliers antes do filtro. O sinal bruto permanece sem o ajuste das médias, então para executar em todos os canais, é importante que y esteja nas interações:
fsinais = matrix(0, nrow(sinais), ncol(sinais))
for (canal in 1:32) {
y = sinais[,canal] - mean(sinais[,canal])
fsinais[,canal]=filter(FILTRO,y)
}Para verificar o sinal bruto e filtrado de cada canal, tirando a média (o exemplo contempla o canal 1):
#Checar o sinal bruto e filtrado
plot((1:nrow(sinais))/HZ,sinais[,1]-mean(sinais[,1]),type="l",xlab="Tempo(s)", ylab="sinal(uV)")
lines((1:nrow(sinais))/HZ,fsinais[,1],col=2)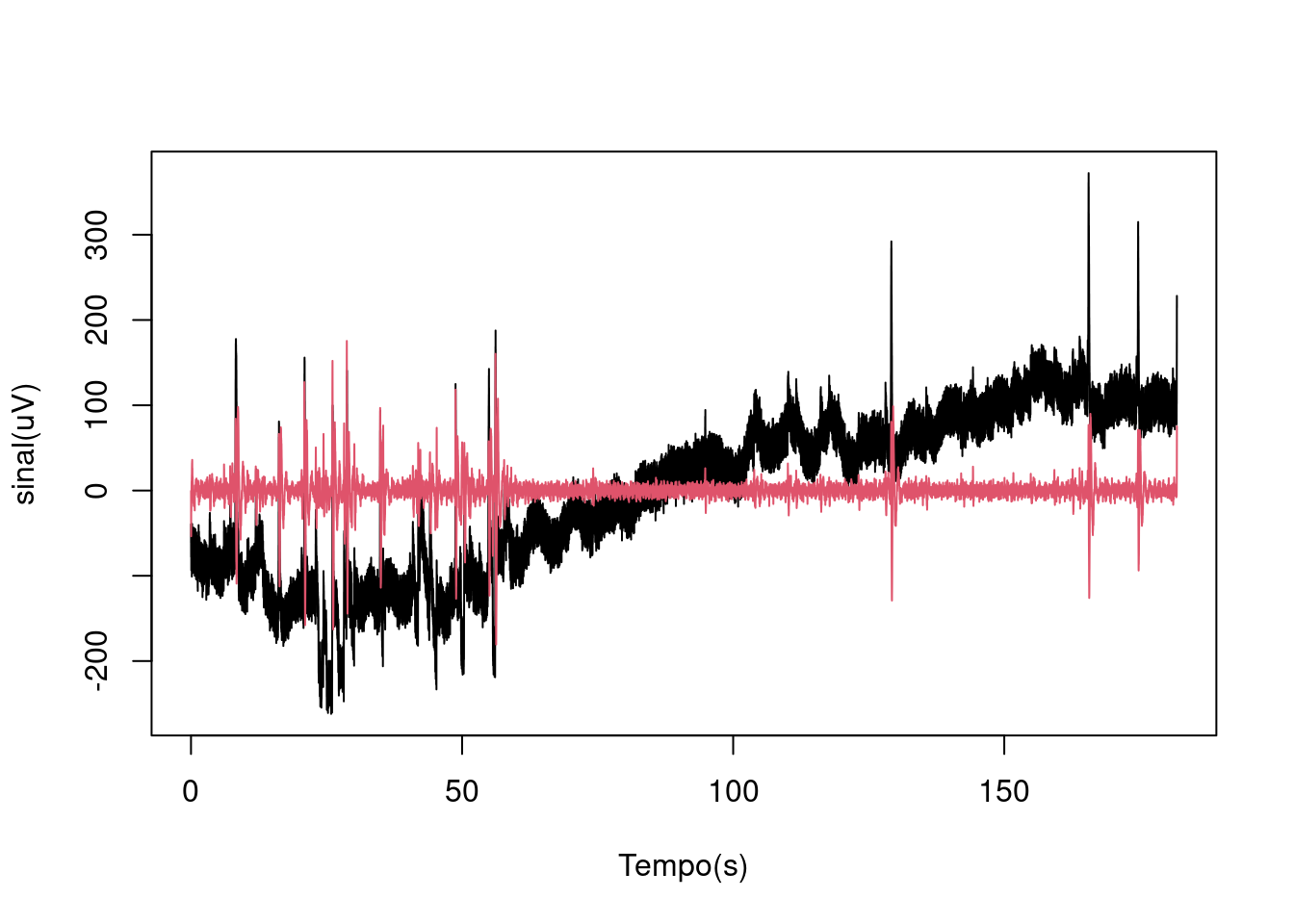
Observações sobre a implementação de filtros: 1. Adicionar a taxa de amostragem atribuindo um valor para HZ.
Passa-baixa em 30hz: ** FILTRO = butter(n=5, W = 30/(HZ/2), type = “low”)
Passa-banda para deixar apenas entre as frequências de 1-40 hz: ** FILTRO = butter(n=5, W = c(1,40)/(HZ/2), type = “pass”)
Passa-alta para frequências acima de 0.2hz: ** FILTRO = butter(n=5, W = 0.2/(HZ/2), type = “high”)